引用筆記本
引用筆記本
本篇文章是使用大型語言模型工具所創建的繁體中文譯本
本篇文章是使用大型語言模型工具所創建的繁體中文譯本
原文出自 Wolfram 社群精選推薦,2025 年 9 月 11 日
原文出自 Wolfram 社群精選推薦,2025 年 9 月 11 日
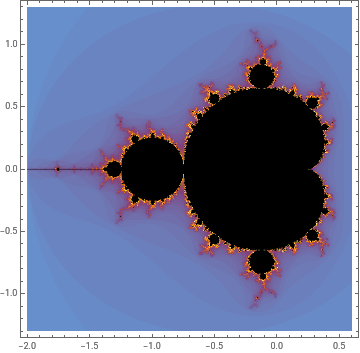
Two views of z ↦ z² + c : Mandelbrot set fractal charts connectivity of related Julia set fractal
Two views of z ↦ z² + c : Mandelbrot set fractal charts connectivity of related Julia set fractal
z ↦ z² + c 的兩種視圖:曼德布洛特分形圖與相關朱利亞集分形的連通性
z ↦ z² + c 的兩種視圖:曼德布洛特分形圖與相關朱利亞集分形的連通性
欲觀看高品質影片與討論,請參考:
𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭 分形可編碼 𝓙𝐮𝐥𝐢𝐚 分形。
關鍵動畫展示:𝓜 中的 𝐰𝐡𝐢𝐭𝐞 𝐝𝐨𝐭 決定 𝓙 的連通性。
儘管用少數符號 𝐙 ↦ 𝐙²+𝐂 定義,無窮分形無法被有限運算完全用盡。任何演算法僅能給出近似值。面對無窮複雜、 可無限探索的宇宙,數學抽象的力量在於能用有限符號形式來表達無限。一些有趣的小知識:
關鍵動畫展示:𝓜 中的 𝐰𝐡𝐢𝐭𝐞 𝐝𝐨𝐭 決定 𝓙 的連通性。
儘管用少數符號 𝐙 ↦ 𝐙²+𝐂 定義,無窮分形無法被有限運算完全用盡。任何演算法僅能給出近似值。面對無窮複雜、 可無限探索的宇宙,數學抽象的力量在於能用有限符號形式來表達無限。一些有趣的小知識:
𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭 和 𝓙𝐮𝐥𝐢𝐚 分形都定義為 𝐙 ↦ 𝐙²+ 𝐂
兩者有何不同?𝓜 繪製的是 𝐂,而 𝓙 繪製的是 𝐙。
白色點(參數 𝐂)會在 𝓜 集(角落)中移動,並且會在中央繪製對應的 𝓙 集。
兩者有何不同?𝓜 繪製的是 𝐂,而 𝓙 繪製的是 𝐙。
白色點(參數 𝐂)會在 𝓜 集(角落)中移動,並且會在中央繪製對應的 𝓙 集。
因此:𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭 是 𝓙𝐮𝐥𝐢𝐚 的地圖集。
這表示 𝓜 集合中的每個點 𝐂(白點)都告訴你對應的 𝓙 集合的結構。如果白點在 𝓜 內部,那麼 𝓙(𝐂) 就是連通的一整體。如果白點在 𝓜 外部,那麼 𝓙(𝐂) 就會碎裂成灰燼。因此,曼德布洛特集就像一張地圖:通過掃描參數空間 𝐂, 你可以對每一個可能的朱利亞的連通性進行分類。
在 Wolfram 語言中,最簡單的程式碼就可以繪製這些分形。例如,下列函數有助於製作這個影片。繪製曼德布洛特集:
In[]:=
MandelbrotSetPlot[]
Out[]=
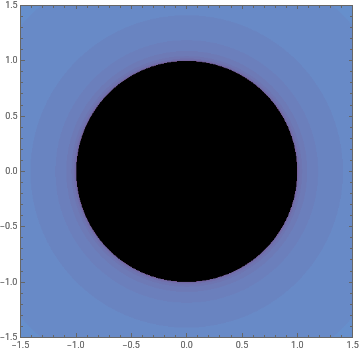
甚至可以為朱利亞集創建互動式應用程式:
In[]:=
Manipulate[JuliaSetPlot[Complex@@p,PlotRange->1.5],{p,Locator},SaveDefinitions->True]
Out[]=
在後續的繪圖或視覺化中,將影像尺寸參數設定為 550:
In[]:=
grSZ=550;
定義一組包含 13 個二維點的列表。這些點能產生美麗的朱利亞圖形。
In[]:=
pts={{-0.205,0.686},{-0.297,0.648},{-0.216,0.707},{-0.2,0.806},{-0.117,0.862},{-0.203,0.811},{-0.218,0.712},{-0.285,0.638},{-0.186,0.653},{-0.086,0.658},{-0.087,0.668},{-0.187,0.673},{-0.187,0.663}};
使用這組點建立一個 B-樣條函數。此函數表示一條平滑曲線,用於插值已知點。它被定義為閉合的,意指曲線曲線的起點和終點相連。
In[]:=
bsp=BSplineFunction@@ResourceFunction["CubicSplineCurve"][pts,SplineClosed->True]
Out[]=
BSplineFunction
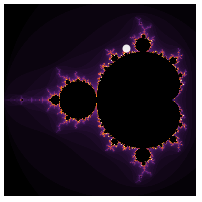
定義一個用於繪製曼德布洛特集合的函數,該集合是在複變動力學中使用的分形。圖中在指定位置包含一個小白圓,可能用於突顯某個有趣的點。這將在後續作為內嵌圖使用。
In[]:=
mand[p_]:=MandelbrotSetPlot[ColorFunction->"SunsetColors",Frame->False,ImageSize->grSZ/3.,Epilog->{White,Disk[p,.01]},PlotRange->{{-.4,0},{.6,1}},PerformanceGoal->"Quality"]mand[{-.35,.7}]
Out[]=
In[]:=
mand2[p_]:=MandelbrotSetPlot[ColorFunction->"SunsetColors",Frame->False,ImageSize->grSZ/3.,Epilog->{White,Disk[p,.05]},PerformanceGoal->"Quality"]mand2[{-.35,.7}]
Out[]=
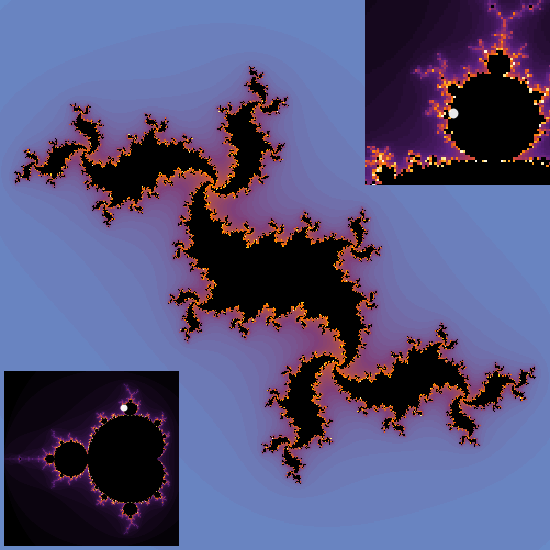
一個 函數用於建立朱利亞集的互動式繪圖。朱利亞集是與複數相關的另一種分形。該圖中包含了之前建立的曼德布洛特集的內嵌圖,並且根據 B-樣條函數動態計算突顯了某些點。這個視覺化讓使用者可以透過調整參數來探索不同的朱利亞集。
In[]:=
Manipulate[JuliaSetPlot[Complex@@bsp[t],ImageSize->grSZ{1,1},PerformanceGoal->"Quality",PlotRange->1.4,Frame->False,Epilog->{Inset[mand[bsp[t]],{Right,Top},{Right,Top}],Inset[mand2[bsp[t]],{Left,Bottom},{Left,Bottom}]}],{t,0,1},SaveDefinitions->True]
Out[]=