[このノートブックは以下のcommunityのポストをLLMツールにより日本語に翻訳したものです：
Wolfram Community，STAFF PICKS，2025年9月11日
​https://community.wolfram.com/groups/-/m/t/3543860]

z ↦ z² + c の2つの見方：Mandelbrot集合フラクタルと関連するJulia集合フラクタルの連結性

by Vitaliy Kaurov
高品質なビデオと解説については，以下をご覧ください:
◼
  • https://www.linkedin.com/feed/update/urn:li:activity:7371542216504291329/
    • ◼
  • https://x.com/superflow/status/1965824573011591264
    • 𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭フラクタルは𝓙𝐮𝐥𝐢𝐚フラクタルを符号化しています．
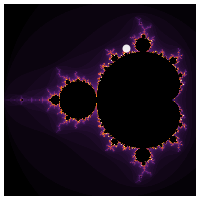
    重要なアニメーションが開発されました：𝓜の中の𝐰𝐡𝐢𝐭𝐞 𝐝𝐨𝐭が𝓙の連結性を定義します．
    少数記号による定義𝐙 ↦ 𝐙²+𝐂にもかかわらず，有限の計算では無限のフラクタル全体を尽くすことはできません．どのようなアルゴリズムでも近似しか得られません．無限に複雑で無限に探索可能な宇宙に直面したとき，数学的抽象化の力は，無限を有限の記号的形で符号化することにあります．いくつかの面白い事実を挙げます：
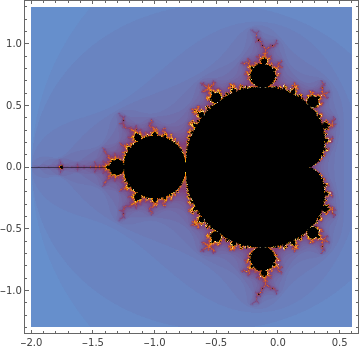
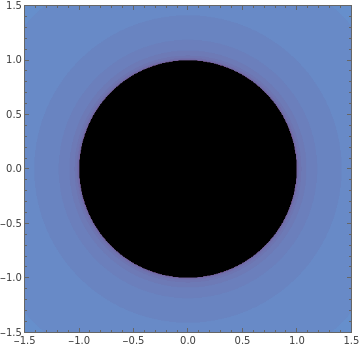
    𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭と𝓙𝐮𝐥𝐢𝐚のフラクタルはどちらも𝐙 ↦ 𝐙²+ 𝐂として定義されます．
    違いは何でしょうか？𝓜は𝐂をプロットし，𝓙は𝐙をプロットします．
    白い点（パラメータ𝐂）は𝓜集合（隅）を移動し，それに対応する𝓙集合が中央にプロットされます．
    したがいまして，𝓜𝐚𝐧𝐝𝐞𝐥𝐛𝐫𝐨𝐭は𝓙𝐮𝐥𝐢𝐚のアトラスです．
    これは，集合𝓜内の各点𝐂（白い点）が，対応する𝓙集合の構造を示しているという意味です．もし白い点が𝓜の内部にあれば，𝓙(𝐂)は一つの連結した全体となります．白い点が𝓜の外側にあれば，𝓙(𝐂)はバラバラに分裂してしまいます．そのため，Mandelbrot集合は地図のように機能します．パラメータ空間𝐂を調べることで，すべての可能なJulia集合を連結性によって分類することができます．
    Wolfram言語では，最も簡単なコードでこれらのフラクタルを描画できます．例えば，以下の関数はこのビデオの作成に役立ちました．マンデルブロ集合をプロットします:
    In[]:=
    MandelbrotSetPlot[]
    Out[]=
    あるいは，Julia向けのインタラクティブなアプリを作成することもできます．
    In[]:=
    Manipulate[JuliaSetPlot[Complex@@p,PlotRange->1.5],{p,Locator},SaveDefinitions->True]
    Out[]=
    ​
    以降のプロットや可視化において，画像サイズのパラメータに550の値を割り当てます．
    In[]:=
    grSZ=550;
    13個の二次元点のリストが定義されています．これらは美しいJulia画像を生成します．
    In[]:=
    pts={{-0.205,0.686},{-0.297,0.648},{-0.216,0.707},{-0.2,0.806},{-0.117,0.862},{-0.203,0.811},{-0.218,0.712},​​{-0.285,0.638},{-0.186,0.653},{-0.086,0.658},{-0.087,0.668},{-0.187,0.673},{-0.187,0.663}};
    この一連の点を使用してB-スプライン関数を作成します．この関数は，指定された点を補間する滑らかな曲線を表します．また，この曲線の開始点と終了点が接続されている，すなわち閉じた形状として定義されています．
    In[]:=
    bsp=BSplineFunction@@ResourceFunction["CubicSplineCurve"][pts,SplineClosed->True]
    Out[]=
    BSplineFunction
    Argument count: 1
    Output dimension: 2
    
    複素力学系で用いられるフラクタルであるMandelbrot集合をプロットする関数が定義されます．このプロットには，関心のある点を強調するためと思われる，指定された位置に小さな白い円盤が含まれています．これは後でインセットとして使用されます．
    In[]:=
    mand[p_]:=MandelbrotSetPlot[ColorFunction->"SunsetColors",Frame->False,ImageSize->grSZ/3.,Epilog->{White,Disk[p,.01]},PlotRange->{{-.4,0},{.6,1}},PerformanceGoal->"Quality"]​​mand[{-.35,.7}]
    Out[]=
    In[]:=
    mand2[p_]:=MandelbrotSetPlot[ColorFunction->"SunsetColors",Frame->False,ImageSize->grSZ/3.,Epilog->{White,Disk[p,.05]},PerformanceGoal->"Quality"]​​mand2[{-.35,.7}]
    Out[]=
    Manipulate
    関数は，複素数に関連した別の種類のフラクタルであるジュリア集合のインタラクティブなプロットを作成するために使用します．このプロットには，先ほど作成したMandelbrot集合のプロットのインセットが含まれており，ハイライトされた点はB-spline関数に基づいて動的に計算されます．この可視化により，パラメータを調整することでさまざまなジュリア集合を探索することができます．
    In[]:=
    Manipulate[​​JuliaSetPlot[Complex@@bsp[t],ImageSize->grSZ{1,1},PerformanceGoal->"Quality",PlotRange->1.4,Frame->False,Epilog->{Inset[mand[bsp[t]],{Right,Top},{Right,Top}],Inset[mand2[bsp[t]],{Left,Bottom},{Left,Bottom}]}]​​,{t,0,1},SaveDefinitions->True]
    Out[]=
    ​
    t

    このノートブックを引用してください

    Two views of z ↦ z² + c: Mandelbrot set fractal charts connectivity of related Julia set fractal​
    by Vitaliy Kaurov​
    Wolfram Community, STAFF PICKS, September 11, 2025
    ​https://community.wolfram.com/groups/-/m/t/3543860