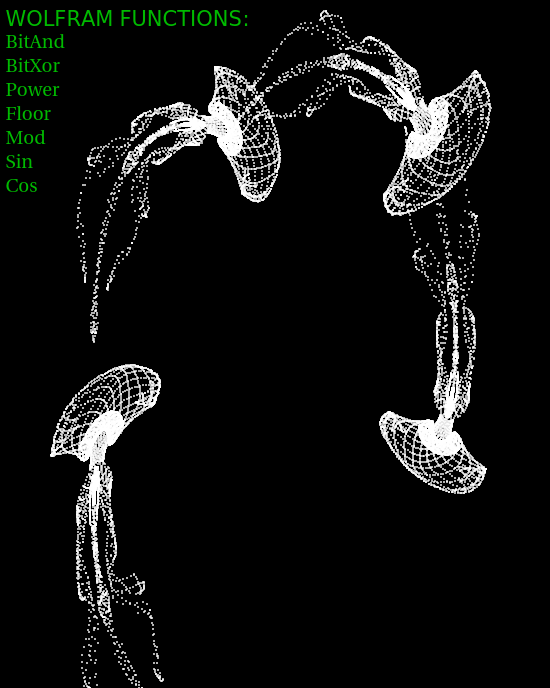
Cuatro medusas: Animacidad aparente en el movimiento de puntos impulsados por funciones matemáticas simples

por Vitaliy Kaurov
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Four medusas: apparent animacy in motion of points driven by simple math functions” producido con ayuda de un LLM y verificado por un traductor profesional
◼
  • Código original de procesamiento JS p5.js: https://x.com/yuruyurau/status/1966894529954673142.
    • ◼
  • Por @yuruyurau https://x.com/yuruyurau
    • a=(y,d=mag(k=(y<9?4+sin(y^8)*9:y/4+cos(y))*cos(i),e=y/6-13)+cos(i/1199)/2)=>point((q=y*k/d*(2+sin(d*2+y-t*16))+79)*cos(c=d/6-t+(i&5))+200,q*d/9*sin(c+i%2*7)+200)
    t=0,draw=$=>{t||createCanvas(w=400,w);background(9).stroke(w,56);for(t+=PI/480,i=2e4;i--;)a(i/980)}

    ANIMACIDAD APARENTE

    Animacidad aparente es la percepción de agencia semejante a la vida a partir de indicios mínimos de movimiento en figuras o puntos por lo demás simples.
    En un cortometraje de 1944, dos triángulos y un círculo se mueven alrededor de una caja. Los espectadores perciben un bravucón, una persecución, un rescate. No hay rostros. Solo movimiento. Estudios posteriores revelaron la receta en señales simples: un punto que comienza por sí solo, acelera o desacelera, gira bruscamente o reacciona a otro punto se percibe como autopropulsado y dirigido a un objetivo. Esas señales son suficientes para que el sistema visual transforme puntos errantes en agentes vivos. Hoy en día, estos marcos conceptuales son herramientas estándar en laboratorios de percepción y en sistemas de IA que intentan inferir objetivos a partir del movimiento.

    CÓDIGO

    Se inicializa el número de puntos (n) que se utilizarán y se crean listas de índices iList y de los valores correspondientes de y
    yList
    .
    n = 20000;​​iList = Range[0, n - 1];​​yList = N[iList/980.];
    Se calculan dos listas para los resultados de la operación AND a nivel de bits y los resultados de la operación módulo para cada índice dividido por 2, luego se calcula el seno de la operación XOR a nivel de bits
    iAnd5 = BitAnd[iList, 5];​​iMod2 = Mod[iList, 2];
    sinXor = N @ Sin[BitXor[Floor[yList], 8]];
    Este código genera la
    sTermList
    , donde cada elemento se calcula en función de una condición aplicada a
    yList
    y
    sinXor
    . Si un elemento de
    yList
    es menor que 9, se utiliza la fórmula
    4 + 9 * sinXor
    ; de lo contrario, se aplica la fórmula
    y / 4 + Cos[y]
    .
    sTermList = MapThread[​​ If[#1 < 9., 4. + 9. #2, #1/4. + Cos[#1]] &,​​ {yList, sinXor}​​];
    kList = sTermList * Cos[N[iList]];​​eList = yList/6. - 13.;​​dBase = Sqrt[kList^2 + eList^2] + Cos[N[iList/1199.]]/2.;
    Se define una función que genere etiquetas de texto en un estilo determinado
    In[]:=
    ClearAll[coner];​​coner[fl_,vo_:.035]:=Prepend​​MapIndexedTextStyle#,19,
    ,FontFamily->"Georgia",Scaled[{.01,.99-vo #2[[1]]}],{Left,Top}&,fl,​​TextStyleToUpperCase@"Wolfram functions:",21,
    ,FontFamily->"DIN Condensed",Scaled[{.01,.99}],{Left,Top}​​
    Se generan etiquetas de texto para algunas funciones utilizadas
    In[]:=
    conLBL=coner[{BitAnd,BitXor,Power,Floor,Mod,Sin, Cos},.035];
    Se define una función que cree un solo fotograma de la animación basado en el tiempo de entrada t.
    (* Single-frame renderer *)​​frame[t_?NumericQ] := Module[​​ {d = dBase, y = yList, k = kList, b5 = N@iAnd5, m2 = N@iMod2, c, q, x, ypix},​​ c = d/6. - t + b5;​​ q = y*k/d*(2. + Sin[d*2. + y - 16. t]) + 79.;​​ x = q*Cos[c] + 200.;​​ ypix = q*d/9.*Sin[c + m2*7.] + 200.;​​ Graphics[​​ {conLBL,PointSize[.0025], White, Opacity[.7],Point[Transpose[{x, ypix}]]},​​ PlotRange -> {{80, 320}, {50, 350}},​​ Background -> Black,​​ ImageSize -> 550​​ ]​​];
    Se crea la animación
    In[]:=
    Manipulate[frame[t],{t,0,2 π },SaveDefinitions->True]
    Out[]=
    ​
    t
    In[]:=
    SetDirectory[NotebookDirectory[]]
    Out[]=
    /Users/vitaliyk/Documents/LiNKEDiN/yuruyurau/*4 medusaas
    Se genera una lista de fotogramas de animación para exportar como un archivo GIF
    frames=Table[frame[t],{t, 0, 2*Pi,2*π/(400.-1)}];
    Export["four_medusas.gif",frames,"DisplayDurations"->.05,ImageSize->550]

    Referencias

    ◼
  • Heider, F., & Simmel, M. (1944). An experimental study of apparent behavior. The American Journal of Psychology, 57(2), 243–259. PDF
    • ◼
  • Tremoulet, P. D., & Feldman, J. (2000). Perception of animacy from the motion of a single object. Perception, 29(8), 943–951. PDF – Journal page
    • ◼
  • Scholl, B. J., & Gao, T. (2013). Perceiving animacy and intentionality: Visual processing or higher-level judgment? In M. D. Rutherford & V. A. Kuhlmeier (Eds.), Social perception: Detection and interpretation of animacy, agency, and intention (pp. 197–230). MIT Press. PDF
    • ◼
  • Gao, T., Newman, G. E., & Scholl, B. J. (2009). The psychophysics of chasing: A case study in the perception of animacy. Cognitive Psychology, 59(2), 154–179. PDF
    • ◼
  • Tremoulet, P. D., & Feldman, J. (2000). Perception of Animacy from the Motion of a Single Object. Perception, 29(8), 943-951. https://doi.org/10.1068/p3101 (Original work published 2000)

    • CITE ESTE CUADERNO

    Cuatro medusas: Animacidad aparente en el movimiento de puntos impulsados por funciones matemáticas simples​
    por Vitaliy Kaurov​
    Comunidad Wolfram, STAFF PICKS, 19 de septiembre de 2025
    ​https://community.wolfram.com/groups/-/m/t/3547363