Complemento de “Base Fibonacci - Numberphile”

Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Companion to "Base Fibonacci - Numberphile"” producido con ayuda de un LLM y verificado por un traductor profesional

Esta publicación de blog explora una representación numérica basada en Fibonacci a través de la perspectiva de un truco de fiesta conocido y su rigurosa base matemática. Partiendo de la representación clásica de Zeckendorf, donde cada entero se escribe de manera única como una suma de números de Fibonacci no consecutivos, reinterpretamos el truco como un problema estructurado de codificación en lugar de un simple juego de manos. Utilizando una tabla indexada por posiciones de Fibonacci, un asistente descompone silenciosamente un número elegido de acuerdo con las posiciones de los 1 en su codificación de Zeckendorf. De manera sorprendente, el anfitrión puede reconstruir el número original leyendo únicamente la primera columna de la tabla, cuyas entradas son los propios números de Fibonacci. Lo que parece ser un truco de fiesta se convierte finalmente en una ilustración concreta de unicidad, restricciones de codificación y la estructura profunda que permanece oculta.

Video de YouTube: https://youtu.be/S5FTe5KP2Cw

Representación de Zeckendorf

La representación de Zeckendorf de un número es una forma única de expresarlo como una suma de números de Fibonacci no consecutivos.
En esta representación, cada número se descompone en una suma en la que no se utilizan dos números de Fibonacci consecutivos, lo que garantiza la unicidad de la representación. Por ejemplo, el número 10 se representaría como

8+2

en términos de números de Fibonacci, ya que

10=8+2

son números de Fibonacci no consecutivos.

Convierta 1 a 100 a la representación de Zeckendorf:

In[]:=

fbZR=ResourceFunction["ZeckendorfRepresentation"]/@Range[100]

Out[]=

{{1},{1,0},{1,0,0},{1,0,1},{1,0,0,0},{1,0,0,1},{1,0,1,0},{1,0,0,0,0},{1,0,0,0,1},{1,0,0,1,0},{1,0,1,0,0},{1,0,1,0,1},{1,0,0,0,0,0},{1,0,0,0,0,1},{1,0,0,0,1,0},{1,0,0,1,0,0},{1,0,0,1,0,1},{1,0,1,0,0,0},{1,0,1,0,0,1},{1,0,1,0,1,0},{1,0,0,0,0,0,0},{1,0,0,0,0,0,1},{1,0,0,0,0,1,0},{1,0,0,0,1,0,0},{1,0,0,0,1,0,1},{1,0,0,1,0,0,0},{1,0,0,1,0,0,1},{1,0,0,1,0,1,0},{1,0,1,0,0,0,0},{1,0,1,0,0,0,1},{1,0,1,0,0,1,0},{1,0,1,0,1,0,0},{1,0,1,0,1,0,1},{1,0,0,0,0,0,0,0},{1,0,0,0,0,0,0,1},{1,0,0,0,0,0,1,0},{1,0,0,0,0,1,0,0},{1,0,0,0,0,1,0,1},{1,0,0,0,1,0,0,0},{1,0,0,0,1,0,0,1},{1,0,0,0,1,0,1,0},{1,0,0,1,0,0,0,0},{1,0,0,1,0,0,0,1},{1,0,0,1,0,0,1,0},{1,0,0,1,0,1,0,0},{1,0,0,1,0,1,0,1},{1,0,1,0,0,0,0,0},{1,0,1,0,0,0,0,1},{1,0,1,0,0,0,1,0},{1,0,1,0,0,1,0,0},{1,0,1,0,0,1,0,1},{1,0,1,0,1,0,0,0},{1,0,1,0,1,0,0,1},{1,0,1,0,1,0,1,0},{1,0,0,0,0,0,0,0,0},{1,0,0,0,0,0,0,0,1},{1,0,0,0,0,0,0,1,0},{1,0,0,0,0,0,1,0,0},{1,0,0,0,0,0,1,0,1},{1,0,0,0,0,1,0,0,0},{1,0,0,0,0,1,0,0,1},{1,0,0,0,0,1,0,1,0},{1,0,0,0,1,0,0,0,0},{1,0,0,0,1,0,0,0,1},{1,0,0,0,1,0,0,1,0},{1,0,0,0,1,0,1,0,0},{1,0,0,0,1,0,1,0,1},{1,0,0,1,0,0,0,0,0},{1,0,0,1,0,0,0,0,1},{1,0,0,1,0,0,0,1,0},{1,0,0,1,0,0,1,0,0},{1,0,0,1,0,0,1,0,1},{1,0,0,1,0,1,0,0,0},{1,0,0,1,0,1,0,0,1},{1,0,0,1,0,1,0,1,0},{1,0,1,0,0,0,0,0,0},{1,0,1,0,0,0,0,0,1},{1,0,1,0,0,0,0,1,0},{1,0,1,0,0,0,1,0,0},{1,0,1,0,0,0,1,0,1},{1,0,1,0,0,1,0,0,0},{1,0,1,0,0,1,0,0,1},{1,0,1,0,0,1,0,1,0},{1,0,1,0,1,0,0,0,0},{1,0,1,0,1,0,0,0,1},{1,0,1,0,1,0,0,1,0},{1,0,1,0,1,0,1,0,0},{1,0,1,0,1,0,1,0,1},{1,0,0,0,0,0,0,0,0,0},{1,0,0,0,0,0,0,0,0,1},{1,0,0,0,0,0,0,0,1,0},{1,0,0,0,0,0,0,1,0,0},{1,0,0,0,0,0,0,1,0,1},{1,0,0,0,0,0,1,0,0,0},{1,0,0,0,0,0,1,0,0,1},{1,0,0,0,0,0,1,0,1,0},{1,0,0,0,0,1,0,0,0,0},{1,0,0,0,0,1,0,0,0,1},{1,0,0,0,0,1,0,0,1,0},{1,0,0,0,0,1,0,1,0,0}}

Verifique el número máximo de elementos en todas las líneas:

In[]:=

resZR=With[{ml1=Max[Length/@fbZR]},Print[ml=ml1];PadLeft[#,ml1]&/@fbZR];

Observe rápidamente los términos:

In[]:=

Short[resZR,5]

Out[]//Short=

{{0,0,0,0,0,0,0,0,0,1},{0,0,0,0,0,0,0,0,1,0},{0,0,0,0,0,0,0,1,0,0},{0,0,0,0,0,0,0,1,0,1},{0,0,0,0,0,0,1,0,0,0},{0,0,0,0,0,0,1,0,0,1},{0,0,0,0,0,0,1,0,1,0},{0,0,0,0,0,1,0,0,0,0},{0,0,0,0,0,1,0,0,0,1},83,{1,0,0,0,0,0,0,1,0,1},{1,0,0,0,0,0,1,0,0,0},{1,0,0,0,0,0,1,0,0,1},{1,0,0,0,0,0,1,0,1,0},{1,0,0,0,0,1,0,0,0,0},{1,0,0,0,0,1,0,0,0,1},{1,0,0,0,0,1,0,0,1,0},{1,0,0,0,0,1,0,1,0,0}}

Conversión de base inversa utilizando álgebra lineal simple:

In[]:=

base=Reverse[Array[Fibonacci,ml,2]]

Out[]=

{89,55,34,21,13,8,5,3,2,1}

Pruebe sobre entradas de términos que terminan en uno:

In[]:=

Select[resZR,#[[-1]]==1&].base

Out[]=

{1,4,6,9,12,14,17,19,22,25,27,30,33,35,38,40,43,46,48,51,53,56,59,61,64,67,69,72,74,77,80,82,85,88,90,93,95,98}

Pruebe sobre entradas de términos en los que el penúltimo término es uno:

In[]:=

Select[resZR,#[[-2]]==1&].base

Out[]=

{2,7,10,15,20,23,28,31,36,41,44,49,54,57,62,65,70,75,78,83,86,91,96,99}

Aplique la conversión de base a cada fila:

In[]:=

resZR2=Table[Select[resZR,#[[-k]]==1&].base,{k,1,ml}]

Out[]=

{{1,4,6,9,12,14,17,19,22,25,27,30,33,35,38,40,43,46,48,51,53,56,59,61,64,67,69,72,74,77,80,82,85,88,90,93,95,98},{2,7,10,15,20,23,28,31,36,41,44,49,54,57,62,65,70,75,78,83,86,91,96,99},{3,4,11,12,16,17,24,25,32,33,37,38,45,46,50,51,58,59,66,67,71,72,79,80,87,88,92,93,100},{5,6,7,18,19,20,26,27,28,39,40,41,52,53,54,60,61,62,73,74,75,81,82,83,94,95,96},{8,9,10,11,12,29,30,31,32,33,42,43,44,45,46,63,64,65,66,67,84,85,86,87,88,97,98,99,100},{13,14,15,16,17,18,19,20,47,48,49,50,51,52,53,54,68,69,70,71,72,73,74,75},{21,22,23,24,25,26,27,28,29,30,31,32,33,76,77,78,79,80,81,82,83,84,85,86,87,88},{34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54},{55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88},{89,90,91,92,93,94,95,96,97,98,99,100}}

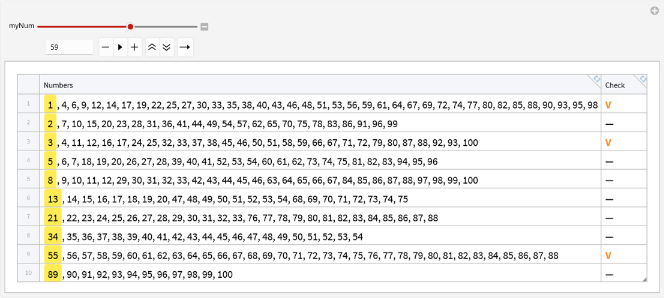
Cree la tabla utilizada en el video y envuélvala con Manipulate para probar todos los números en el rango dado:

In[]:=

Manipulate[myNum2=myNum;ToTabular[<|"Numbers"->Row[Riffle[highlightHead@#,", "]],"Check"->If[MemberQ[#,myNum],Style["V",Bold,StandardOrange],Missing[]]|>&/@resZR2,ItemSize->{{73,5},0.8}],{myNum,1,100,1},SaveDefinitions->True]

Out[]=

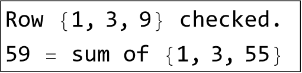
Sincronice la salida con el control deslizante de arriba y recupere el número adivinado a partir de la posición de las marcas de verificación:

In[]:=

Dynamic[With[{pos=Flatten@Position[Reverse@ResourceFunction["ZeckendorfRepresentation"][myNum2],1]},Row[{"Row ",pos," checked. \n",myNum2," = sum of ",Fibonacci[pos+1]}]]]//Framed

Out[]=

Representación dual de Zeckendorf

Luego extendemos la discusión a una representación dual de Fibonacci, regida por una restricción complementaria que prohíbe los términos faltantes de Fibonacci adyacentes. Aunque visualmente es similar, esta regla dual produce una estructura combinatoria distinta. Utilice un código similar al anterior

In[]:=

fb2=ResourceFunction["DualZeckendorfRepresentation"]/@Range[100];

La longitud máxima es menor en esta representación:

In[]:=

res=With[{ml1=Max[Length/@fb2]},Print[ml=ml1];PadLeft[#,ml1]&/@fb2];

Conversión de base hacia atrás usando álgebra lineal simple:

In[]:=

base=Reverse@Array[Fibonacci,ml,2]

Out[]=

{55,34,21,13,8,5,3,2,1}

Convierta la codificación binaria de vuelta a las representaciones decimales:

In[]:=

resDZR=Table[Select[res,#[[-k]]==1&].base,{k,1,ml}];

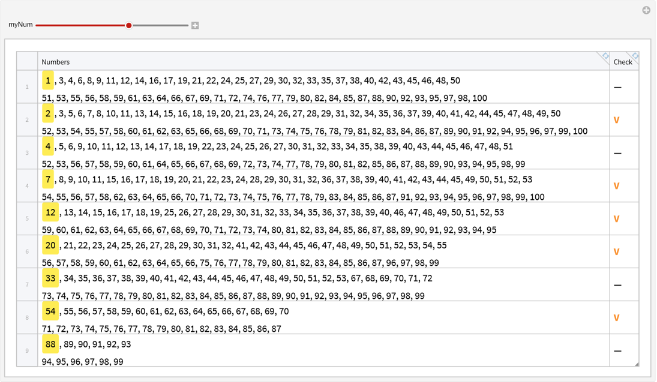
Cree la tabla de trucos de fiesta similar a la anterior pero utilizando la representación dual:

In[]:=

Manipulate[myNum3=myNum;ToTabular[<|"Numbers"->Column@(Row[Riffle[#,", "]]&/@Partition[highlightHead@#,Floor[Length[#]/2]]),"Check"->If[MemberQ[#,myNum],Style["V",Bold,StandardOrange],Missing[]]|>&/@resDZR,ItemSize->{{78,3},2},Alignment-><|"Rows"->Center|>,ImageSize->{850,800}],{myNum,1,100,1}]

Out[]=

Recupere el número adivinado a partir de la posición de las marcas de verificación:

Arte de portada

Incrustación de grafo de Hamming para la rep. de Zeckendorf:

Utilidad

CITE ESTE CUADERNO

Complemento de “Base Fibonacci - Numberphile”
por Shenghui Yang
Comunidad Wolfram, STAFF PICKS, 11 de enero de 2025
https://community.wolfram.com/groups/-/m/t/3604657