Cambio de variables de estado para procesos estocásticos generales
Cambio de variables de estado para procesos estocásticos generales
por Bruno Tenorio
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Change of state variables for general stochastic processes” producido con ayuda de un LLM y verificado por un traductor profesional
Este cuaderno aborda el problema de cambiar variables en ecuaciones diferenciales estocásticas generales (EDE) tanto para procesos de Stratonovich como de Ito. Utilizamos dos funciones personalizadas para analizar ejemplos clave y aplicaciones físicas, destacando la capacidad de aplicar transformaciones de coordenadas nominales y examinar explícitamente los términos simbólicos resultantes.
Funciones del repositorio de funciones
Funciones del repositorio de funciones
Con respecto a los detalles de cómo se realizan las transformaciones, se recomienda consultar la documentación de Wolfram Function Repository:
Para procesos de Stratonovich:
In[]:=
ResourceFunction["StratonovichProcessChangeVariables"]
Out[]=
Para procesos de Ito:
In[]:=
ResourceFunction["ItoProcessChangeVariables"]
Out[]=
Cambio de variables para un proceso de Stratonovich
Cambio de variables para un proceso de Stratonovich
Casos de uso
Casos de uso
Transformación cuadrática
Transformación cuadrática
Defina un proceso de Stratonovich:
In[]:=
procX=StratonovichProcess1,σExp[-],{x,x0},t
2
x
2
x
Out[]=
StratonovichProcess,σ,x[t],{{x},{x0}},{t,0}
1
2
x[t]
-
2
x[t]
Transformación cuadrática del proceso:
In[]:=
transformed=[procX,y,y==x^2];
Verifique que sea un proceso válido:
In[]:=
ProcessParameterQ[transformed]
Out[]=
True
Imprima los términos transformados de deriva y difusión:
In[]:=
Print["Drift: ",transformed["Drift"],"\nDiffusion: ",transformed["Diffusion"]]
Drift: -Diffusion: -2σ
2
y[t]
-y[t]
y[t]
Transformación cúbica de un proceso de Wiener
Transformación cúbica de un proceso de Wiener
Comience con un proceso de Stratonovich que tiene una forma de proceso de Wiener:
In[]:=
proc=StratonovichProcess[{0,1},{x,x0},t]
Out[]=
StratonovichProcess[{{0},{{1}},x[t]},{{x},{x0}},{t,0}]
Transformación cúbica de un proceso:
In[]:=
Out[]=
StratonovichProcess{0},3,y[t],{{y},{}},{t,0}
2/3
y[t]
3
x0
Escalado temporal
Escalado temporal
Comience con un proceso general con deriva a y difusión b:
In[]:=
spLinear=StratonovichProcess[{a,b},{x,x0},{t,t0}]
Out[]=
StratonovichProcess[{{a},{{b}},x[t]},{{x},{x0}},{t,t0}]
Escalado de variables de proceso:
In[]:=
resTimeDep=spLinear,{y},y
x
t
Out[]=
StratonovichProcess,,{y[t]},{y},,{t,0}
a-y[t]
t
b
t
x0
t0
Proceso de deriva cero a partir de Ornstein-Uhlenbeck
Proceso de deriva cero a partir de Ornstein-Uhlenbeck
Defina el siguiente proceso de OrnsteinUhlenbeck:
In[]:=
ou=StratonovichProcess@OrnsteinUhlenbeckProcess[μ,σ,θ,x0]
Out[]=
StratonovichProcessθμ-x.t.,{{σ}},x.t.,{x.},{x0},t.,0
Considere la transformación y = (x-μ) que depende del tiempo:
θt
ⅇ
In[]:=
transformed=ou,y,y(x.-μ);
θt.
Compruebe que el proceso no tenga deriva para esta transformación:
In[]:=
transformed["Drift"]=={0}
Out[]=
True
Transformación tangente/Cauchy
Transformación tangente/Cauchy
Comience con un proceso de Stratonovich que tenga la forma de un proceso de Wiener:
In[]:=
procX=StratonovichProcess[{0,1},{x,0},t];
Realice la transformación :
y=Tan(x)
In[]:=
Out[]=
StratonovichProcess[{{0},{{}},y[t]},{{y},{0}},{t,0}]
2
Sec[ArcTan[y[t]]+π]
1
Especifique una rama de solución para :
0<=x<2π
In[]:=
procY=[procX,y,y==Tan[x],Assumptions->{0<=x<2π}]
Out[]=
StratonovichProcess[{{0},{{1+}},y[t]},{{y},{0}},{t,0}]
2
y[t]
Coordenadas cilíndricas a esféricas
Coordenadas cilíndricas a esféricas
Defina un proceso en coordenadas cilíndricas:
In[]:=
proc3D=StratonovichProcess[{{1/ρ,0,0},{σ/(ρ^2+z^2),0,σz}},{{ρ,ϕ,z},{ρ0,ϕ0,z0}},t]
Out[]=
StratonovichProcess,0,0,+,{0},{σz[t]},{ρ[t],ϕ[t],z[t]},{{ρ,ϕ,z},{ρ0,ϕ0,z0}},{t,0}
1
ρ[t]
σ
2
z[t]
2
ρ[t]
Realice una transformación a coordenadas esféricas usando la notación de nombres largos:
In[]:=
Out[]=
StratonovichProcess,,0,σr[t]+,σCosθ.[t]-Sinθ.[t],{0},r[t],θ.[t],φ[t],r,θ.,φ,+,ArcTan[z0,ρ0],ϕ0,{t,0}
1
r[t]
Cotθ.[t]
2
r[t]
2
Cosθ.[t]
σSinθ.[t]
2
r[t]
1
3
r[t]
2
z0
2
ρ0
Aplicaciones de física
Aplicaciones de física
Movimiento de atrapamiento estocástico en 2D
Movimiento de atrapamiento estocástico en 2D
Define a stochastic process representing harmonic oscillator trap(including a magnetic effect) in Cartesian coordinates:
Defina un proceso estocástico que represente una trampa de oscilador armónico (incluyendo un efecto magnético) en coordenadas cartesianas:
In[]:=
spMagnetic=StratonovichProcess[{{-γx+By,-γy-Bx},{{σ,0},{0,σ}}},{{x,y},{x0,y0}},t]
Out[]=
StratonovichProcess[{{-γx[t]+By[t],-Bx[t]-γy[t]},{{σ,0},{0,σ}},{x[t],y[t]}},{{x,y},{x0,y0}},{t,0}]
Cambie a coordenadas polares que sean más adecuadas para el problema:
In[]:=
spPolar=[spMagnetic,{r,ϕ},"Cartesian"->"Polar"]
Out[]=
StratonovichProcess{-γr[t],-B},{σCos[ϕ[t]],σSin[ϕ[t]]},-,,{r[t],ϕ[t]},{r,ϕ},+,ArcTan[x0,y0],{t,0}
σSin[ϕ[t]]
r[t]
σCos[ϕ[t]]
r[t]
2
x0
2
y0
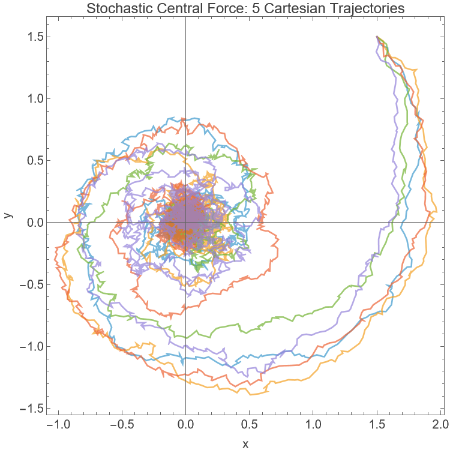
Configure los parámetros y simule 5 trayectorias:
In[]:=
paths=RandomFunction[spPolar/.{γ->0.5,B->2,σ->0.2,x0->1.5,y0->1.5},{0,20,0.01},5];
Vuelva a las coordenadas cartesianas para representar:
In[]:=
cartesianPaths=TimeSeriesMap[{#[[1]]Cos[#[[2]]],#[[1]]Sin[#[[2]]]}&,paths];
Represente las trayectorias:
In[]:=
ListLinePlotcartesianPaths["ValueList"],
Out[]=
Flujo celular con difusión
Flujo celular con difusión
Defina un proceso de Stratonovich que represente el flujo de partículas especificado por la deriva con fluctuaciones térmicas añadidas:
Visualice el diagrama de flujo del desplazamiento:
Representación de líneas de corriente de deriva u-v transformadas:
Visualice 10 trayectorias en el espacio u-v:
Cambio de variables para un proceso de Ito
Cambio de variables para un proceso de Ito
Casos de uso
Casos de uso
Transformada logarítmica de un proceso de movimiento browniano geométrico
Transformada logarítmica de un proceso de movimiento browniano geométrico
Construya un proceso de Ito a partir de un proceso estocástico de movimiento browniano:
Obtenga el movimiento browniano aritmético mediante una transformación logarítmica:
Muestre la FDP del proceso:
Transformación exponencial
Transformación exponencial
Defina un proceso de Ito que represente un proceso de Wiener:
Realice una transformación exponencial:
Media y varianza del proceso:
Podemos obtener un resultado equivalente para la media y la varianza del proceso usando TransformedProcess:
Desplazamiento de la media en un proceso de Ornstein-Uhlenbeck
Desplazamiento de la media en un proceso de Ornstein-Uhlenbeck
Defina el proceso de OrnsteinUhlenbeck:
Calcule la media y la varianza del proceso:
Verifique la media y la varianza; la media se desplazó, pero el proceso sigue siendo OrnsteinUhlenbeck:
Usando TransformedProcess:
Coordenadas polares
Coordenadas polares
Comience con un proceso de Wiener bidimensional:
Transforme el proceso a coordenadas polares. Observamos que la deriva inicial nula se vuelve no nula y depende únicamente del radio en coordenadas polares:
Transformación dependiente del tiempo
Transformación dependiente del tiempo
Cree un proceso de Ito en particular:
Transformación explícita dependiente del tiempo:
Cambio de variable tangente hiperbólica
Cambio de variable tangente hiperbólica
Comience con un proceso sin deriva:
Transformada del coseno
Transformada del coseno
Defina un proceso de Wiener unidimensional:
Realice un cambio trigonométrico de variables, ya que debido a la naturaleza periódica de la transformación no es posible obtener una solución única:
Aplicaciones de física
Aplicaciones de física
Oscilador armónico con ruido
Oscilador armónico con ruido
Defina un proceso que represente la posición y la velocidad de una partícula, donde la deriva en la velocidad está relacionada con la posición (como en la ley de Hooke). Con difusión agregada solo en la velocidad:
Al transformar a las variables E y ϕ (energía y fase), estamos suponiendo masa unitaria:
Configure los parámetros:
Al representar el retrato de fases, obtenemos trayectorias circulares deformadas:
Si visualizamos las trayectorias en el espacio de energía-fase utilizando los mismos parámetros, la línea discontinua representa la energía sin ruido:
Difusión del estado cuántico
Difusión del estado cuántico
Realice el cambio de variables a coordenadas esféricas, que son más apropiadas para la geometría del espacio de estados:
Calcule las trayectorias del vector de Bloch en coordenadas cartesianas:
Las probabilidades cuánticas según la regla de Born pueden obtenerse con un histograma de la componente z del vector de Bloch para muchas trayectorias, suponiendo que el tiempo sea lo suficientemente largo como para producir el colapso al estado propio
CITE ESTE CUADERNO
CITE ESTE CUADERNO
Cambio de variables de estado para procesos estocásticos generales
por Bruno Tenorio
Comunidad Wolfram, STAFF PICKS, 20 de enero de 2026
https://community.wolfram.com/groups/-/m/t/3609731
por Bruno Tenorio
Comunidad Wolfram, STAFF PICKS, 20 de enero de 2026
https://community.wolfram.com/groups/-/m/t/3609731