International Essays |
Un juego completamente nuevo: Teoría de juegos en Wolfram Language 14.2
Un juego completamente nuevo: Teoría de juegos en Wolfram Language 14.2
25 de febrero de 2025
Marc Vicuna, Desarrollador de kernel, I&D de algoritmos
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “A Whole New Ball Game: Game Theory in Wolfram Language 14.2” producido con ayuda de un LLM y verificado por un traductor profesional
¿Desea tomar decisiones óptimas frente a la competencia? ¿Quiere analizar contextos competitivos y predecir los resultados de eventos competitivos? ¿Necesita elaborar estrategias y planes frente a la adversidad y poner su efectividad a prueba? ¿O simplemente estudia pregrado y lucha por entender un curso obligatorio de teoría de juegos en la universidad?
El nuevo conjunto de funciones de teoría de juegos de Wolfram le permitirá generar, experimentar, probar, resolver y visualizar cualquier evento utilizando teoría de juegos.
Historia de la teoría de juegos Originalmente, la teoría de juegos se limitaba a juegos de azar simples. Estos comparten algunas características en común: solo involucran dos jugadores a la vez y, o bien un jugador gana y el otro pierde, o ambos jugadores tienen una ganancia de cero. Estos juegos se conocen hoy como juegos de suma cero entre dos jugadores.
Si definimos la teoría de juegos en función de la elaboración de estrategias óptimas, esta podría ser tan antigua como los juegos de azar. Debemos este análisis temprano (¡Y la teoría de la probabilidad!) al famoso polímata y apostador Girolamo Cardano. Alternativamente, si la definimos en función del análisis de juegos basado en las posibles acciones de todos los jugadores, entonces podríamos atribuir su origen a James Waldegrave, por su análisis del juego Le Her en 1713, donde se dieron soluciones de estrategia minimax.
Por supuesto, los juegos pueden ser más que solo entretenimiento. Después de todo, pocos juegos pueden afirmar tener una base de jugadores tan grande como el juego de la economía. Antoine-Augustin Cournot, en su investigación de 1838 sobre los principios matemáticos de la teoría de la riqueza (Recherches sur les principes mathématiques de la théorie des richesses), descubrió soluciones a la competencia de precios que posteriormente serían denominados equilibrios de Nash.
Sin embargo, la mayoría de estos descubrimientos están algo aislados, y usualmente se consideran como meros precursores del tema moderno. La teoría de juegos comienza oficialmente con el libro de John von Neumann de 1944, Theory of Games and Economic Behavior, en el cual se acuñó el término “teoría de juegos” y se determinaron sus axiomas, estableciéndola de esta manera como su propio campo. Este resumen general de la historia de la teoría de juegos no estaría completo sin mencionar a John Nash, cuyo teorema de existencia de los equilibrios de Nash transformó la teoría de juegos unos pocos años después, en 1950.
Como podemos imaginar, este campo de estudio ha crecido enormemente desde entonces. La teoría de juegos moderna se resume mejor como las matemáticas de la toma de decisiones. En esencia, estudia el comportamiento de jugadores humanos, animales y artificiales en todo tipo de competencia. Herbert Gintis lo dijo mejor:
“La teoría de juegos trata tanto sobre cómo las personas cooperan que de cómo compiten... La teoría de juegos trata sobre la aparición, transformación, difusión y estabilización de formas de comportamiento.”
Juegos de matriz: Gato y ratón Los juegos de matriz también se conocen como juegos simultáneos. En efecto, estos juegos se caracterizan por la simultaneidad de las acciones de todos los jugadores. Como su nombre lo indica, los juegos de matriz se basan en matrices. Para ser precisos, cualquier juego de matriz de jugadores puede expresarse mediante un arreglo de dimensiones, donde la última dimensión es un vector de ganancias para todos los jugadores.
n
n+1
Se pueden generar juegos de matriz mediante la nueva función en la versión 14.2. Por ejemplo, el siguiente es un juego de dos jugadores en el cual cada jugador tiene una elección entre dos acciones:
game=MatrixGame[{{1,-1},{-1,1}}]
Out[]=
MatrixGame
Este juego es un juego de suma cero, como se puede ver en el que representa las ganancias para cada jugador:
game["Dataset"]
Out[]=
|
Usamos una ganancia de 1 para representar la victoria y una ganancia de –1 para representar la derrota. Por lo tanto, en este juego, el primer jugador gana cuando las acciones de ambos jugadores coinciden, y el segundo jugador gana cuando las acciones no coinciden.
Si bien los juegos simultáneos suelen expresarse en términos de matrices, estas rápidamente se vuelven difíciles de leer a medida que aumenta el número de jugadores y acciones. Por lo tanto, nuestro equipo desarrolló para visualizar esta clase de juegos:
MatrixGamePlot[game]
Out[]=
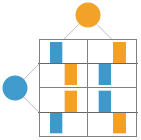
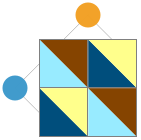
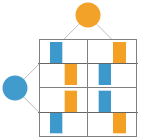
MatrixGamePlot y otras funciones están diseñadas para funcionar con juegos que tengan cualquier número de jugadores. Es posible que “SplitSquare” le parezca un diseño sea más intuitivo para juegos de dos jugadores, mientras que los juegos con más de dos jugadores se visualizan mejor usando el diseño predeterminado "BarChart":
{MatrixGamePlot[game,PlotLayout->"SplitSquare"],MatrixGamePlot[game,PlotLayout->"BarChart"]}
Out[]=
,
Por buenas que sean estas visualizaciones, es difícil deducir la historia detrás de este juego solo a partir de visualizaciones generales. Para facilitar la interpretación, consideremos dos jugadores: un gato y un ratón. El gato puede buscar en la casa o en el jardín, y el ratón puede esconderse en la casa o en el jardín. Por supuesto, el gato gana si está en el mismo lugar que el ratón, y si no están en el mismo lugar, gana el ratón.
El conjunto de datos y la representación para la versión de gato y ratón del juego pueden ser más fáciles de leer especificando GamePlayerLabels y GameActionLabels en este juego:
In[]:=
CatAndMouse=MatrixGame{{1,-1},{-1,1}},;
{CatAndMouse["Dataset"],CatAndMouse["Plot"]}
Out[]=
,
|
Por supuesto, los gatos son perezosos. Parece más probable que nuestro gato sea demasiado sedentario como para salir de la casa (🏠) por un simple ratón. Sabiendo esto, un ratón oportunista debería elegir ir siempre al jardín (🌿), ya que esto debería llevar a una ganancia mayor. Para verificarlo, el ratón debería usar en este juego y estrategia, lo cual le permite calcular las ganancias esperadas de un juego según una estrategia dada:
MatrixGamePayoff[game,{{1,0},{0,1}}]
Out[]=
{-1,1}
¿Y si el gato no es perezoso? Algunos gatos tienen esos ojos místicos, impredecibles, un rostro de póker perfecto. Para nuestro ratón, parece que este gato hará lo que sea necesario para ganar. El ratón debe replantear su estrategia, volverla estable y sólida, y asegurarse de que sea al menos tan probable ganar para él como para el gato. El ratón usa para probar todas las estrategias en las que cada animal elige entre la casa o el jardín, y verificar si una estrategia en particular es un equilibrio de Nash. Lamentablemente, parece que todos los casos son inestables y que el gato podría tener la ventaja:
Table[VerifyMatrixGameStrategy[game,{{cat,1-cat},{mouse,1-mouse}}],{cat,0,1},{mouse,0,1}]
Out[]=
{{False,False},{False,False}}
Nuestro ratón tiene un último as bajo la manga: ! Esta poderosa función es nuestro solucionador de juegos que calcula equilibrios de Nash, es decir, estrategias que ninguno de los jugadores tiene interés en cambiar. Usando esta herramienta, el ratón se da cuenta de que su salvación está en la aleatoriedad:
Esta estrategia es mixta, donde la probabilidad de algunas acciones no es 0 ni 1. En este caso, el ratón tendrá que lanzar una moneda: si sale cara, se queda en la casa; si sale cruz, irá al jardín. Cabe mencionar que el gato no puede aprovecharse de esta estrategia, por lo cual su mejor estrategia también es un 50/50.
Ciertamente, hasta ahora el juego es poco realista. Es probable que el ratón tenga muchos más lugares para esconderse y que el gato tenga muchos más lugares para buscar. Esto implicaría que cada jugador tenga más de dos acciones, y de hecho hay otros juegos en los cuales esto sucede. Por ejemplo, en el juego de la Morra, cada jugador tiene 50 posibles acciones. Todas las funciones vistas anteriormente se pueden generalizar a este o cualquier número de acciones.
Por supuesto, no puede considerarse una fiesta cuando solo juegan dos jugadores a la vez. También se pueden especificar juegos de matriz como el bar El Farol con cualquier número de jugadores, aunque no le desearía tantos ratones ni a mi peor enemigo:
Si la colonia se rebela, el país tiene la opción de otorgar la independencia o reprimir la rebelión. Dado que perder una colonia es costoso, el país siempre tiene un mayor interés en reprimir la rebelión, como se muestra al comparar la segunda ganancia de cada resultado:
Incluso solo en términos de teoría de juegos, es evidente que el país tiene la ventaja en este juego. A menudo en juegos de árbol, es el jugador que juega al final quien tiene la ventaja, ya que la ganancia se elige directamente. En este caso, sin importar lo que haga la colonia, el país puede asegurar una ganancia positiva simplemente eligiendo reprimir e imponer impuestos, dependiendo de la acción de la colonia:
Por supuesto, los juegos de árbol pueden tener más de dos acciones consecutivas. Por ejemplo, consideremos este juego llamado Centipede, cuyo nombre todavía me resulta un misterio:
Los juegos de árbol tampoco están limitados a dos jugadores. Por ejemplo, consideremos un juego de herencia donde seguimos el cactus dorado heredado que pertenecía al abuelo Zubair a lo largo de toda su familia:
Resulta bastante difícil deducir el significado y la utilidad de un juego solo a partir de una lista de ganancias. Dado que cada juego tiene su propia historia, origen, peculiaridades y propiedades, quisimos permitir a los usuarios explorar la riqueza de la teoría de juegos con juegos bien curados directamente desde el lenguaje. De esta manera, cada juego cuenta con funcionalidades útiles que permiten a cualquiera comprenderlo, investigarlo y caracterizarlo. Puede encontrar una descripción textual del juego:
Aprenda acerca de sus orígenes en la literatura:
Encuentre las clases de juegos a las que pertenece:
Y, por supuesto, juéguelo:
Un paso adelante Sabemos que la teoría de juegos puede parecer algo críptica para los no iniciados. En este sentido, nuestro primer objetivo con estas características de teoría de juegos es facilitar el proceso de construir y explorar juegos, manteniéndolo preciso y útil. Mediante documentación extensa y accesible, todas estas características se han alineado con el carácter divertido e interesante de los juegos:
De hecho, hemos dedicado mucho esfuerzo a la documentación de estas funciones. La cantidad de ejemplos, explicaciones y consideraciones detalladas de incluso las características más mínimas va mucho más allá de la documentación típica para nuevas características al momento de su lanzamiento. Este nivel de documentación debería permitirle comenzar con la teoría de juegos en cuestión de minutos:
Los enlaces a todos estos recursos están disponibles en un solo lugar para permitir a los usuarios tener una perspectiva general de esta funcionalidad:
¡No llegue tarde al juego y pruebe estas nuevas características por su cuenta!