Computation models in e-origami system Eos
Computation models in e-origami system Eos
Tetsuo Ida
University of Tsukuba, Japan
https : // www .i-eos.org/ida/
https : // www .i-eos.org/ida/
First of all, I would like to congratulate SYNASC 2021, the 21 st edition of the symposia . Thanks are due to the organizers of SYNASC at West University of Timisoara and RISC, JKU . I feel happy to be back at SYNASC and feel honored to have an opportunity of delivering an invited talk .
Keywords
Keywords
computational origami and e-origami system Eos
Suppose that we practice origami to create a shape of interest. Furthermore, we also want to consider origami as a process of creation in the era of digital transformation.
We interact with a computer to create the intended shape in the computer's memory and visualize it on the computer's screen.
Advantages of this approach are
Advantages of this approach are
improved precision of shapes
Ability of reasoning properties of the created structures
deference to other kinds of DX processes such as manufacturing by 3D printing.
Motivation (concerning model)
Motivation (concerning model)
In 2020, subject “Programming” was introduced to the curriculum of Japanese elementary schools. It is a compulsory subject to all children.
Programming is to write down, in sequence, sentences of some languages that computers can understand, so that we can let computers do the task we ask.
IT venders are quick to react to this new initiative and develop teaching materials (mostly software products).
Although this initiative may be a step towards further modernization of Japanese education system, there is a big concern about what to teach in the subject of “programming.”
A fundamental question is “What is a computer for the children?”
A computer can be iPad, Surface, laptop, Nintendo machine, smartphone, abacus, calculator, or even children’s mother, pet, or robot.
We have to have a model of a computer for programming, since most of them are too complex (sophisticated) to speak to in simple expressions.
Unless we have a solid model of a computer in our mind, it is very difficult to write a program for that computer.
We develop the ability of modeling as we grow by learning mathematics (arithmetic), natural sciences, engineering etc. The ability of modeling develops rapidly around the age of 15 - 18 years. Development of the ability of modeling and applying it to everyday life is our life long endeavor.
"Algorithm " would have been an adequate subject.
Languages
Languages
We designed language called Orikoto. It is a subset of Wolfram Language (WL) of Mathematica.
WL is based on the concept of term rewriting.
Orikoto is a command language, but is based on an abstract origami (AO) rewrite system on the structure AO defined by binary relations (adjacency, superposition) on the set of faces.
Orikoto expressions are translated to those of other languages whose semantics can be interpreted easily by the languages (of computers or mathematics).
statements of Huzita-Justin rules (of paper folding)
expressions of a variant of first-order predicate logic
polynomial rings over the field of rational functions
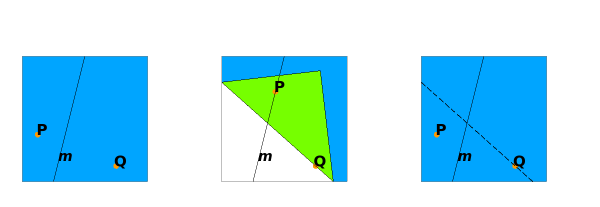
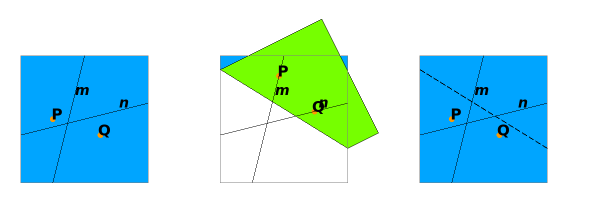
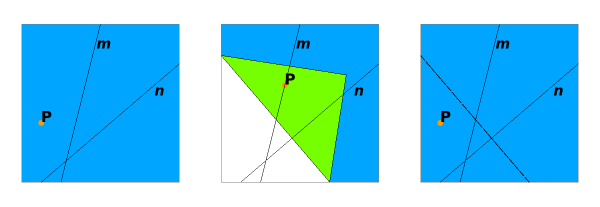
Huzita-Justin rule (set)
Huzita-Justin’s rule set is defined by the superposition of lines and points (constructed by intersection of lines) with appropriate degeneracy and non-incident conditions. It is a complete enumeration of operations made possible by two superpositions. It consists of seven rules.
Axiom
Axiom
Huzita - Justin rules specify fold-lines that we can perform a fold by hand.
Huzita - Justin rules
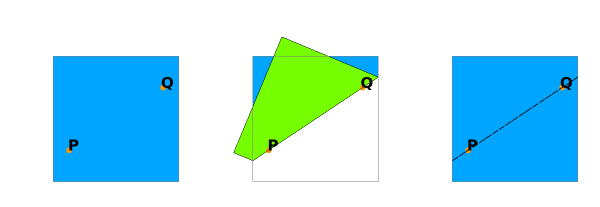
O1
O1
Out[]=
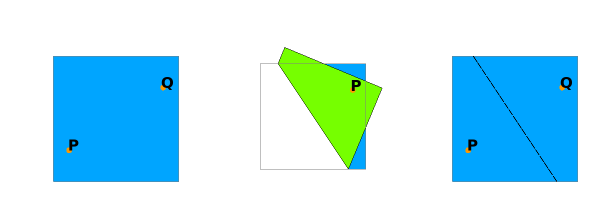
O2
O2
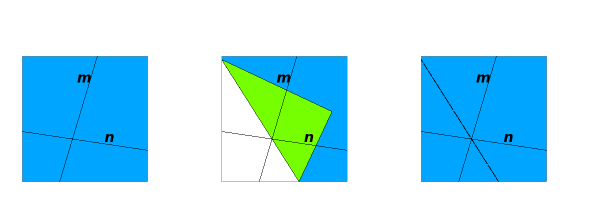
O3
O3
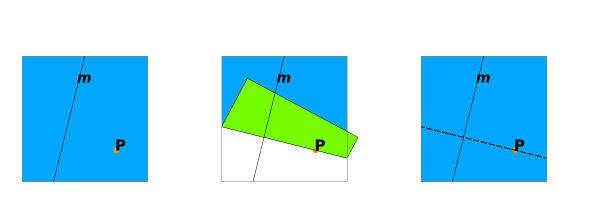
O4
O4
O5
O5
O6
O6
O7
O7
Example - Angle trisection
Example - Angle trisection
Construction
Construction
In[]:=
EosSession["Angle trisector"];
In[]:=
NewOrigami[10];NewPoint["E"{7,8}]
Angle trisector: Step 1
Out[]=
We select the third one and obtain the origami shown below.
The rest of the commands help us to view the obtained trisectors.
The graphics output below more clearly shows the trisectors.
Verification
We end the current session by EndSession[];
On verification of Eos
On verification of Eos
Verification of Eos is to prove that the constructed object satisfies a desired properties. Eos is built over symbolic and algebraic systems and the same data structures are used in the entire system. Thanks to this, we can streamline the process of construction-visualization-verification. Let us take look at
Traditional Origami
Traditional Origami
To many people, origami is fun!
More complicated methods of folding are used.
In addition to Huzita-Justin folds, we have many fold methods. They are combinations of Huzita-Justin folds
Compositional origami force us to access to the power of algebraic and graph theoretic techniques.
Towards 3D origami and variations
Towards 3D origami and variations
Origami piano
Origami piano
A 2D origami would not be rendered an exciting illustration with a textured sheet of origami. We use semi-3D modeling of origami here. We perform twice “squash fold” as well. This origami construction is beyond Huzita-Justin’s.
The next example illustrates the semi-3D origami with texture mapping. Nowadays, we can buy at shops of stationery goods a set of origami sheets with beautiful patterns. The purpose of this example is to show that Eos incorporates the capability of using this kind of pattern on the surface of the face of an origami.
Origami piano
Origami piano
https : // www . wolframcloud . com/obj/ida . tetsuo . ge/Published/Origami - Piano - presentation - pub . nb
Concluding Remarks
Concluding Remarks
Overview of Eos system
Formalization of Computational Origami
is discussed in detail in the monograph:
An Introduction to Computational Origami, Springer, 2020
is discussed in detail in the monograph:
An Introduction to Computational Origami, Springer, 2020