Journeys
Journeys
A few weeks ago, a friend of mine sent me his solution to a coding challenge he worked on. I was intrigued by the challenge and the other greate solutions and decided to try to do a solution in Wolfram Language, my favorite problem exploration tool :)
The challenge
The challenge
The problem is from a Mike Hadlow tweet and originated from a job interview one of his friends had. The full challenge is stated on his GitHub page, and restated here:
You are given a file, something like this:
1 1 E
RFRFRFRF
1 1 E
3 2 N
FRRFLLFFRRFLL
3 3 N
0 3 W
LLFFFLFLFL
2 4 S
RFRFRFRF
1 1 E
3 2 N
FRRFLLFFRRFLL
3 3 N
0 3 W
LLFFFLFLFL
2 4 S
It contains zero to many (in this case 3) journeys. Here’s the first one:
1 1 E
RFRFRFRF
1 1 E
RFRFRFRF
1 1 E
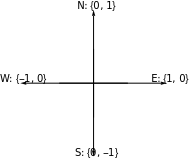
Each one starts with the initial coordinates of the robot (1 1 in this case) and the direction it is pointing in. In this case E = East. The directions are as follows:
N = North
E = East
S = South
W = West
E = East
S = South
W = West
Following the starting conditions are a list of commands:
RFRFRFRF
Each character is a command, either to turn (L = left, R = right) or to move forwards (F).
Finally the journey ends with another set of coordinates and a direction. This is the expected position and orientation of your robot at the end of the journey. Your program should check that it ends at the specified coordinates and facing in the given direction.
The challenge is to parse the input file, set the start position of your robot, then have it execute the instructions and check its final position with the expected position.
Solution
Solution
Let’s start by importing the sample journeys and examine the first one.
In[]:=
sampleFile="https://raw.githubusercontent.com/mikehadlow/Journeys/master/Journeys/input.txt";
In[]:=
journeySamples=StringSplit[Import[sampleFile],"\n\n"];journey1=journeySamples[[1]]
Out[]=
1 1 ERFRFRFRF1 1 E
Here the start position is {1,1} and the direction is East. By converting the direction to a vector value, the problem can be transformed to a vector rotation problem.
In[]:=
directionMap={"E"{1,0},"S"{0,-1},"W"{-1,0},"N"{0,1}};
Out[]=
To get the robots state, we define a helper function that parse the state string to a tuple of the from {position,direction }
In[]:=
parseState[s_String]:=StringSplit[s," "]/.{x_,y_,v_}{{ToExpression@x,ToExpression@y},v/.directionMap}
Let’s try to parse the robot’s start state for the first journey
In[]:=
parseState["1 1 E"]
Out[]=
{{1,1},{1,0}}
To reverse the state back to a string we define
In[]:=
stateToString[{{x_,y_},v_}]:=StringTemplate["`1` `2` `3`"][x,y,v/.(Reverse/@directionMap)]
In[]:=
stateToString[{{1,1},{1,0}}]
Out[]=
1 1 E
Next it’s possible to define a parser for a full journey
In[]:=
parseJourney[s_String]:= StringSplit[s,"\n"]/.{init_,cmd_,res_} <|"initPos"parseState@init,"commands"cmd,"result"parseState@res|>
If we try it out on the first journey we get
In[]:=
parseJourney@journey1
Out[]=
initPos{{1,1},{1,0}},commandsRFRFRFRF,result{{1,1},{1,0}}
Now it’s possible define a command step as a transformation of the robot state. When we have a rotation command we are actually rotating the direction vector, “Right” is by -90 ° and “Left” is +90° . We can do that with a vector and rotation matrix multiplication, here Wolfram Language has a very convenient function for creating a rotation matrix.
In[]:=
step[{pos_,v_},"R"]:={pos,RotationMatrix[-90°].v}step[{pos_,v_},"L"]:={pos,RotationMatrix[90°].v}
When we move “Forward” we just add the direction vector to our current position.
step[{pos_,v_},"F"]:={pos+v,v}
If we try it out with the first 3 steps of journey1 we get
In[]:=
step1=step[{{1,1},{1,0}},"R"]
Out[]=
{{1,1},{0,-1}}
In[]:=
step2=step[step1,"F"]
Out[]=
{{1,0},{0,-1}}
In[]:=
step3=step[step1,"R"]
Out[]=
{{1,1},{-1,0}}
To travel a full journey
travel[journey_]:=FoldList[step,journey["initPos"],Characters@journey["commands"]]
Traveling the first journey we get
In[]:=
stateToString/@(travel@parseJourney@journey1)//TableForm
Out[]//TableForm=
1 1 E |
1 1 S |
1 0 S |
1 0 W |
0 0 W |
0 0 N |
0 1 N |
0 1 E |
1 1 E |
Transforming the problem to the vector domain, resulted in a compact and readable solution. An added benefit is it’s very general, so it can support command with arbitrary degrees of rotations, for example “ Right 35° ” .
With a working prototype, it would be trivial to transform the solution to a code language with a descent matrix library, for example Python or C#.
With a working prototype, it would be trivial to transform the solution to a code language with a descent matrix library, for example Python or C#.
Final code
Final code
In[]:=
directionMap = {"E"{1,0},"S"{0,-1},"W"{-1,0},"N"{0,1}};parseState[s_String] := StringSplit[s," "] /. {x_,y_,v_} {{ToExpression@x,ToExpression@y},v/.directionMap}stateToString[{{x_,y_},v_}] := StringTemplate["`1` `2` `3`"][x,y,v/.(Reverse/@directionMap)]parseJourney[s_String] := StringSplit[s,"\n"] /. {init_,cmd_,res_} <|"initPos"parseState@init,"commands"cmd,"result"parseState@res|>step[{pos_,v_},"R"] := {pos,RotationMatrix[-90°].v}step[{pos_,v_},"L"] := {pos,RotationMatrix[90°].v}step[{pos_,v_},"F"] := {pos+v,v}travel[journey_] := FoldList[step, journey["initPos"], Characters@journey["commands"]]
Tests
Tests
Verify that all the samples have the expected result.
In[]:=
VerificationTest[Last@travel[#],#result]&/@parseJourney/@journeySamples//TestReport
Out[]=
TestReportObject