Introduction to Wolfram Mathematica: particle in one-dimensional box
Introduction to Wolfram Mathematica: particle in one-dimensional box
Wolfram Mathematica Desktop (it’s paid) and its online version Wolfram Cloud (basic version is free) are a symbolic and numerical computing environment. Such products are extremely useful for solving physics and mathematics problems. We used them to study quantum mechanical problems.
If you don’t have the paid version of Wolfram Mathematica Desktop alternatively you can use the basic version of Wolfram Cloud (Mathematics online) for free.
To use Wolfram Cloud you need to have a Wolfram ID (Wolfram account), if you do not yet have an Wolfram ID you must “sign up for free” at the page www.wolframcloud.com.
If you are reading this document for the first time, then you are reading the document in your web browser (e.g. Chrome or Firefox. Microsoft Edge is not supported) and then you are using Wolfram Cloud (note that the URL of the opened page starts with www.wolframcloud.com ).
If you have the paid version of Wolfram Mathematica Desktop, you can download the notebook from the menu item at the top right “Download”.
If you have signed in to Wolfram Cloud, you can access a simple tutorial using the menu item at the top right Intro \ Elementary Introduction Book
Another simple tutorial is “Fast introduction for math students”, it can be found at page www.wolfram.com/language/fast-introduction-for-math-students/en/.
Below we will see a very very brief introduction to the use of Mathematica, but you need to read at least one of the previous tutorials.
The document-files processed by Mathematica (both Desktop and Online versions) are called notebook and the file extension is nb, for example the name of this file is “0_Introduction_To_Mathematica.nb”.
Wolfram System notebooks consist of lists of Cell objects.
The two most important cell types are input cell and output cell.
A input cell is a space where you can enter one or more instructions for Mathmatica to execute.
Mathematica executes commands in input cell only when you Click in the cell (to activate the cell) and use the Shift-Enter command or alternatively when using the menu item Evaluation \ Evaluate Cells. (You can too execute all the cells of the notebook with a single command using the menu item Evaluation \ Evaluate All Cells).
Usually, immediately after processing an input cell, an output cell appears, containing the output produced by Mathematica.
Note that the string In[*] appears on the left side of each Input cell. While the string Out[*] appears on the left side of the Output cell.
You cannot process or modify this document (notebook) because you are not the owner of it, so to proceed you must make a copy. To do this you have to use the top entry Make Your Own Copy. If you have not signed in to the site of Wolfram Cloud, the site will ask you to sign in. At that point you will have created your copy of the notebook that you can use and edit. Your copy was created in the path “Home \ Copied Files”.
To browse your files you have to use the Cloud Files window. To open or close the Cloud Files window you need to use the Cloud Files top menu item. To open your new file, you just created, open the Cloud Files window and open (with a double click) the Copied Files folder. In this folder you will find your new file “0_Introduction_To_Mathematica.nb”.
IMPORTANT NOTE: from now on, to open your notebook you have to Sign In to Wolfram Cloud at URL www.wolframcloud.com, if necessary open Cloud Files window (seen on the right side), open the Copied Files folder: in it you will find your notebook.
(After opening the notebook, you can copy the URL, which you see in the browser, to quickly access it later).
In this notebook we analyze the simple case of the quantum particle confined in a one-dimensional box. Particle is confined to an interval (one-dimensional box) of the x axis, in the range [0, L].
In this notebook, for simplicity, we do not solve the Schröedinger equation but we immediately write the solutions and show that they satisfy the Schröedinger equation.
The Schröedinger equation is solvable only for the discrete values of the Energy En[n], they are all possible values for energy.
Each solution φ[n,x] represents a physical state and it is associated with its respective energy En[n].
In the following input cell we define in Mathematica the function En[n] which has as its argument the positive integer n (n=1,2,3...) and which provides the energy levels. As the value of the variable n varies, I have all energy levels: En[1], En[2], En[3], ...
After having defined in Mathematica the function En[n] , we can then use it when we need it, for example to obtain the energy of level 3, we can simply write En [3].
NOTE. Whether the notebook is opened with Mathematica Desktop or opened with Mathematica Online (Cloud), to process the “active cell” (the line in which the cursor blinks) it is sufficient to use the command “Shift + Enter” (or alternatively you can use the menu item “Evaluation \ Evaluate Cells”).
Now, click on the following formula (to activate the cell) and use the Shift-Enter command, immediately after this cell the output cell will appear in which the formula appears, this indicates that Mathematica has processed the cell: in this case the output of Mathematica consists simply of repeating the contents of the formula.
If you don’t have the paid version of Wolfram Mathematica Desktop alternatively you can use the basic version of Wolfram Cloud (Mathematics online) for free.
To use Wolfram Cloud you need to have a Wolfram ID (Wolfram account), if you do not yet have an Wolfram ID you must “sign up for free” at the page www.wolframcloud.com.
If you are reading this document for the first time, then you are reading the document in your web browser (e.g. Chrome or Firefox. Microsoft Edge is not supported) and then you are using Wolfram Cloud (note that the URL of the opened page starts with www.wolframcloud.com ).
If you have the paid version of Wolfram Mathematica Desktop, you can download the notebook from the menu item at the top right “Download”.
If you have signed in to Wolfram Cloud, you can access a simple tutorial using the menu item at the top right Intro \ Elementary Introduction Book
Another simple tutorial is “Fast introduction for math students”, it can be found at page www.wolfram.com/language/fast-introduction-for-math-students/en/.
Below we will see a very very brief introduction to the use of Mathematica, but you need to read at least one of the previous tutorials.
The document-files processed by Mathematica (both Desktop and Online versions) are called notebook and the file extension is nb, for example the name of this file is “0_Introduction_To_Mathematica.nb”.
Wolfram System notebooks consist of lists of Cell objects.
The two most important cell types are input cell and output cell.
A input cell is a space where you can enter one or more instructions for Mathmatica to execute.
Mathematica executes commands in input cell only when you Click in the cell (to activate the cell) and use the Shift-Enter command or alternatively when using the menu item Evaluation \ Evaluate Cells. (You can too execute all the cells of the notebook with a single command using the menu item Evaluation \ Evaluate All Cells).
Usually, immediately after processing an input cell, an output cell appears, containing the output produced by Mathematica.
Note that the string In[*] appears on the left side of each Input cell. While the string Out[*] appears on the left side of the Output cell.
You cannot process or modify this document (notebook) because you are not the owner of it, so to proceed you must make a copy. To do this you have to use the top entry Make Your Own Copy. If you have not signed in to the site of Wolfram Cloud, the site will ask you to sign in. At that point you will have created your copy of the notebook that you can use and edit. Your copy was created in the path “Home \ Copied Files”.
To browse your files you have to use the Cloud Files window. To open or close the Cloud Files window you need to use the Cloud Files top menu item. To open your new file, you just created, open the Cloud Files window and open (with a double click) the Copied Files folder. In this folder you will find your new file “0_Introduction_To_Mathematica.nb”.
IMPORTANT NOTE: from now on, to open your notebook you have to Sign In to Wolfram Cloud at URL www.wolframcloud.com, if necessary open Cloud Files window (seen on the right side), open the Copied Files folder: in it you will find your notebook.
(After opening the notebook, you can copy the URL, which you see in the browser, to quickly access it later).
In this notebook we analyze the simple case of the quantum particle confined in a one-dimensional box. Particle is confined to an interval (one-dimensional box) of the x axis, in the range [0, L].
In this notebook, for simplicity, we do not solve the Schröedinger equation but we immediately write the solutions and show that they satisfy the Schröedinger equation.
The Schröedinger equation is solvable only for the discrete values of the Energy En[n], they are all possible values for energy.
Each solution φ[n,x] represents a physical state and it is associated with its respective energy En[n].
In the following input cell we define in Mathematica the function En[n] which has as its argument the positive integer n (n=1,2,3...) and which provides the energy levels. As the value of the variable n varies, I have all energy levels: En[1], En[2], En[3], ...
After having defined in Mathematica the function En[n] , we can then use it when we need it, for example to obtain the energy of level 3, we can simply write En [3].
NOTE. Whether the notebook is opened with Mathematica Desktop or opened with Mathematica Online (Cloud), to process the “active cell” (the line in which the cursor blinks) it is sufficient to use the command “Shift + Enter” (or alternatively you can use the menu item “Evaluation \ Evaluate Cells”).
Now, click on the following formula (to activate the cell) and use the Shift-Enter command, immediately after this cell the output cell will appear in which the formula appears, this indicates that Mathematica has processed the cell: in this case the output of Mathematica consists simply of repeating the contents of the formula.
In[]:=
En[n_]=
1
2m
2
nπℏ
L
Out[]=
2
n
2
π
2
ℏ
2m
2
L
In the following input cell we define the function φ[n,x] solution of the Schröedinger equation.
The function φ[n,x] has as its argument the positive integer n and the variable x (which is the position variable of the particle).
As n varies, I have all the solutions: φ[1,x], φ[2,x], φ[3,x], ... All functions are real.
The function φ[n,x] is defined only within the interval [0, L] so outside this interval it must be considered null.
Click on the following formula (to activate the cell) and use the Shift-Enter command, immediately after this cell an output cell will appear in which the formula appears, this indicates that Mathematica has processed the cell.
The function φ[n,x] has as its argument the positive integer n and the variable x (which is the position variable of the particle).
As n varies, I have all the solutions: φ[1,x], φ[2,x], φ[3,x], ... All functions are real.
The function φ[n,x] is defined only within the interval [0, L] so outside this interval it must be considered null.
Click on the following formula (to activate the cell) and use the Shift-Enter command, immediately after this cell an output cell will appear in which the formula appears, this indicates that Mathematica has processed the cell.
In[]:=
φ[n_,x_]=Sin
2
L
nπx
L
Out[]=
2
1
L
nπx
L
The functions En[n] and φ[n,x] are defined for each value of the positive integer n, for which En[1] returns the first energy level and the relative wave function is obtained with φ[1,x]. We repeat that the functions are null outside the range [0, L].
Click on the following formula (to activate the cell) and use the Shift-Enter command, immediately after this cell an output cell will appear in which the formula appears, this indicates that Mathematica has processed the cell. NOTE that this time the output cells are 2 because there were two different instructions in the input cell: En[n] and φ[n,x].
Click on the following formula (to activate the cell) and use the Shift-Enter command, immediately after this cell an output cell will appear in which the formula appears, this indicates that Mathematica has processed the cell. NOTE that this time the output cells are 2 because there were two different instructions in the input cell: En[n] and φ[n,x].
In[]:=
En[1]φ[1,x]
Out[]=
2
π
2
ℏ
2m
2
L
Out[]=
2
1
L
πx
L
IMPORTANT NOTE. From now on we will not repeat it anymore that to process each single cell you have to click on the cell (to activate the cell) and use the Shift-Enter command or alternativity you can use the menu item “Evaluation \ Evaluate Cells”. As an alternative to processing all cells one by one, you can use the menu item Evaluation \ Evaluate All Cells to process all the cells of the notebook.
Now we find the energy value of the first 3 levels n = 1, 2, 3.
Now we find the energy value of the first 3 levels n = 1, 2, 3.
In[]:=
En[1]En[2]En[3]
If you want to easily compare energy levels or draw functions it is useful to set values for constants . We make the following settings .
NOTE: in the following case the output cell was not produced because the lines end with the symbol semicolon “;”. The semicolon at the end of a command asks Mathematica to process the input cell but not to produce an output cell.
NOTE: in the following case the output cell was not produced because the lines end with the symbol semicolon “;”. The semicolon at the end of a command asks Mathematica to process the input cell but not to produce an output cell.
In[]:=
ℏ=1;m=1;L=1;
Now we find again the energy value of the first 3 levels n = 1, 2, 3.
This time the constants (ℏ,m,L) no longer appear.
This time the constants (ℏ,m,L) no longer appear.
In[]:=
En[1]En[2]En[3]
Out[]=
2
π
2
Out[]=
2
2
π
Out[]=
9
2
π
2
If we want the results in numeric format, we can add the statement “// N” at the end of each line. Only then is it easy to compare values.
In[]:=
En[1]//NEn[2]//NEn[3]//N
Out[]=
4.9348
Out[]=
19.7392
Out[]=
44.4132
Now we show the first three solutions of Schröedinger' s equation.
In[]:=
φ[1,x]φ[2,x]φ[3,x]
Out[]=
2
Sin[πx]Out[]=
2
Sin[2πx]Out[]=
2
Sin[3πx]We show the graph of the three functions. Note that functions are drawn only inside the interval [0, L] since outside that interval the functions are null .
In[]:=
Plot[φ[1,x],{x,0,L}]Plot[φ[2,x],{x,0,L}]Plot[φ[3,x],{x,0,L}]
Out[]=
Out[]=
Out[]=
In[]:=
The square modulus of the functions φ[1,x], φ[2,x] , φ[3,x] give the probability density of the x, so the functions must be normalized, that is, the following integrals must return the value 1.
Here we compute the integral over the whole dimension of the interval[0, L], which effectively gives the value 1.
Here we compute the integral over the whole dimension of the interval[0, L], which effectively gives the value 1.
In[]:=
Integrate[,{x,0,L}]Integrate[,{x,0,L}]Integrate[,{x,0,L}]
2
Abs[φ[1,x]]
2
Abs[φ[2,x]]
2
Abs[φ[3,x]]
Out[]=
1
Out[]=
1
Out[]=
1
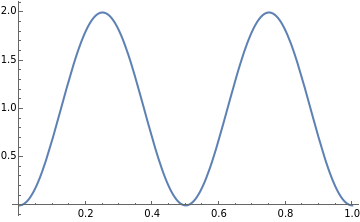
We graph the three probability densities of the x
In[]:=
Plot[,{x,0,L}]Plot[,{x,0,L}]Plot[,{x,0,L}]
2
Abs[φ[1,x]]
2
Abs[φ[2,x]]
2
Abs[φ[3,x]]
Out[]=
Out[]=
We calculate the average value of the variable x.
As in classical mechanics, the average value is the center of the box, 1/2 since the size of the box is L = 1.
As in classical mechanics, the average value is the center of the box, 1/2 since the size of the box is L = 1.
The square modulus of the functions c[1,p], c[2,p], c[3,p] give the probability density of the x, so the functions must be normalized, that is, the following integrals must return the value 1.
For performance purposes only, in the following cell we use approximate “numeric integration” using the NIntegrate statement (note that the statement starts with the letter N) instead of using analytic exact integration using the Integrate statement (note that the instruction begins with the letter I).
We have chosen the integration range [-30, +30] by observing the previous graphs. In fact, only in this range are the functions significantly different from zero.
Since the result is approximate, the value is not exactly 1, but a value very close to 1.
The approximation error decreases if the integration interval is extended, for example try with the range [-1000, + 1000].
For performance purposes only, in the following cell we use approximate “numeric integration” using the NIntegrate statement (note that the statement starts with the letter N) instead of using analytic exact integration using the Integrate statement (note that the instruction begins with the letter I).
We have chosen the integration range [-30, +30] by observing the previous graphs. In fact, only in this range are the functions significantly different from zero.
Since the result is approximate, the value is not exactly 1, but a value very close to 1.
The approximation error decreases if the integration interval is extended, for example try with the range [-1000, + 1000].