WOLFRAM NOTEBOOK

​
Slide
1
of
24

I teoremi del valor medio
di Rolle, Lagrange e Cauchy

Gianluca Gorni
Università di Udine, www.dimi.uniud.it/gorni
7 maggio 2020
"Michel Rolle (1652–1719)"
Giuseppe Luigi Lagrange (1736–1813)
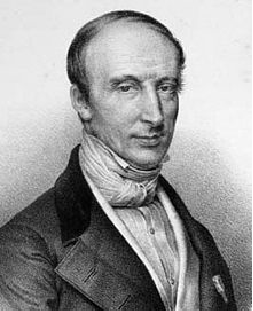"Augustin-Louis Cauchy (1789–1857)"
​
Slide
2
of
24
​
Parte I
Il teorema di Rolle
Out[]=
​
Slide
3
of
24

Il teorema di Rolle

Enunciato del teorema:

Supponiamo che sia dato un intervallo chiuso e limitato
[a,b]
sull’asse delle ascisse:
Out[]=
e una funzione
f:[a,b]
Out[]=
tale che
◼
  • f
    sia continua su tutto l’intervallo 
    [a,b]
    (estremi compresi),
    • ◼
  • f
    sia derivabile sull’intervallo aperto 
    ] a,b[
    (agli estremi non importa se è derivabile o no),
    • ◼
  • nei due estremi la
    f
    abbia lo stesso valore:
    f(a)=f(b)
    .
    • Out[]=
    Allora esiste almeno un punto
    c∈]a,b[
    Out[]=

    Fine dell’enunciato.

    ​
    Slide
    4
    of
    24

    Esploriamo il teorema di Rolle

    Istruzioni per l’uso

    Nel pannello precedente si può cambiare la funzione trascinando i piccoli cerchietti:
    Si può spostare anche il punto grande a sinistra; insieme si sposterà anche il punto grande a destra, rimanendo alla stessa quota.
    Si possono aggiungere cerchietti con Alt + Click (su Windows) oppure con ⌘ + Click (sul Macintosh).
    Se il grafico dovesse uscire dal pannello, lo si può comprimere muovendo il cursore.
    ​
    Slide
    5
    of
    24

    Esploriamo 2

    Quando il grafico dovesse uscire dal pannello, lo si può comprimere muovendo il cursore:
    ​
    Slide
    6
    of
    24

    Esploriamo 3

    ​
    Slide
    7
    of
    24
    ma ce ne può essere anche più di uno, per esempio 3:
    o più:
    ​
    Slide
    8
    of
    24

    Togliendo un’ipotesi alla volta…

    ​
    Slide
    9
    of
    24

    Dimostrazione del teorema di Rolle

    Dimostreremo il teorema di Rolle combinando opportunamente
    ◼
  • il teorema di Weierstraß sull’esistenza del massimo e minimo globale e
    • ◼
  • il teorema di Fermat sulla derivata nei punti di massimo e minimo locali interni.
    • e la funzione è continua. Il teorema di Weierstraß si applica.
    Consideriamo l'insieme dei valori assunti:
    Vediamo di precisare l’idea.
    ​
    Slide
    10
    of
    24
    ​
    Slide
    11
    of
    24
    ​
    Slide
    12
    of
    24
    ​
    Slide
    13
    of
    24
    ​
    Slide
    14
    of
    24

    Conclusione della dimostrazione

    Il teorema è quindi dimostrato.

    Osservazione

    Si potrebbe dare una dimostrazione costruttiva del teorema di Rolle, ma sarebbe più complicata.
    ​
    Slide
    15
    of
    24
    Parte II
    Il teorema del valor medio di Lagrange
    ​
    Slide
    16
    of
    24

    Premessa: la corda per i punti estremi

    consideriamo il segmento che congiunge gli estremi del grafico (detto anche corda o secante):
    Qual’è la pendenza della corda? La formula è
    Ci interessa anche l’equazione della corda (come retta, non come segmento).
    ​
    Slide
    17
    of
    24

    Il teorema del valor medio di Lagrange

    Enunciato del teorema:

    tale che

    Fine dell’enunciato.

    Chiarimento

    ◼
  • e la corda che passa per gli estremi del grafico
    • sono parallele.
    ​
    Slide
    18
    of
    24

    Esploriamo il teorema di Lagrange

    Istruzioni per l’uso

    Nel pannello precedente si può cambiare la funzione trascinando i piccoli cerchietti:
    Si possono aggiungere cerchietti con Alt + Click (su Windows) oppure con ⌘ + Click (sul Macintosh).
    ​
    Slide
    19
    of
    24

    Esploriamo Lagrange 2

    ​
    Slide
    20
    of
    24

    Esploriamo Lagrange 3

    ​
    Slide
    21
    of
    24

    Dimostrazione: (1) la funzione ausiliaria

    Il grafico della funzione ausiliaria è in verde nelle figure seguenti:
    La formula della funzione ausiliaria è quindi
    ​
    Slide
    22
    of
    24
    cioè
    come volevasi dimostrare.
    ​
    Slide
    23
    of
    24
    Parte III
    Il teorema del valor medio di Cauchy

    Enunciato del teorema:

    tali che

    Interpretazione geometrica (cenno)

    ​
    Slide
    24
    of
    24

    Fine

    Wolfram Cloud

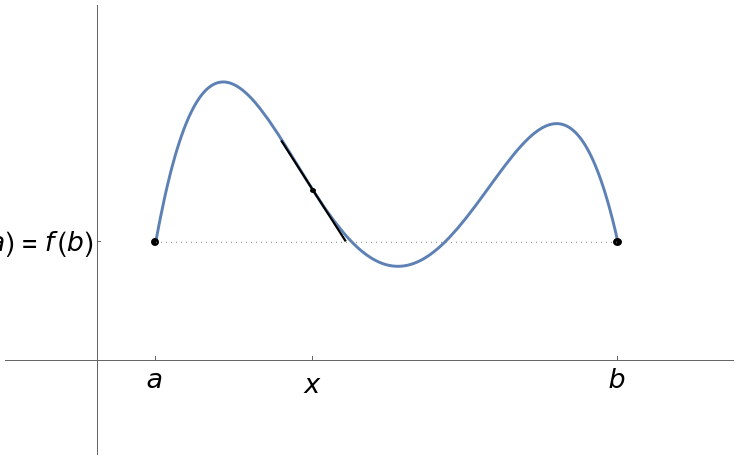
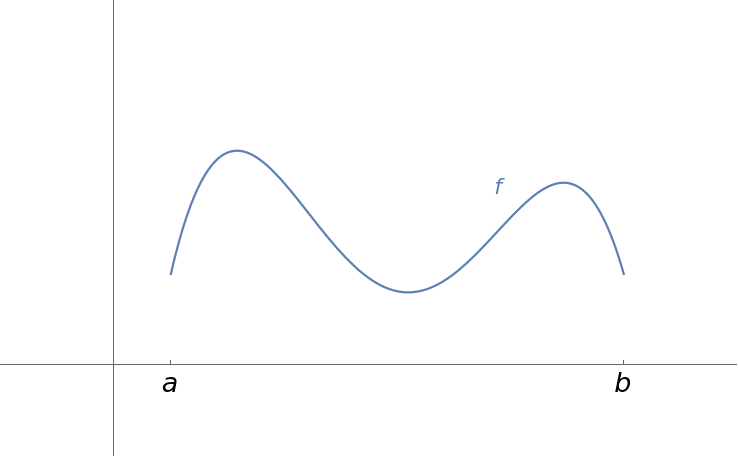
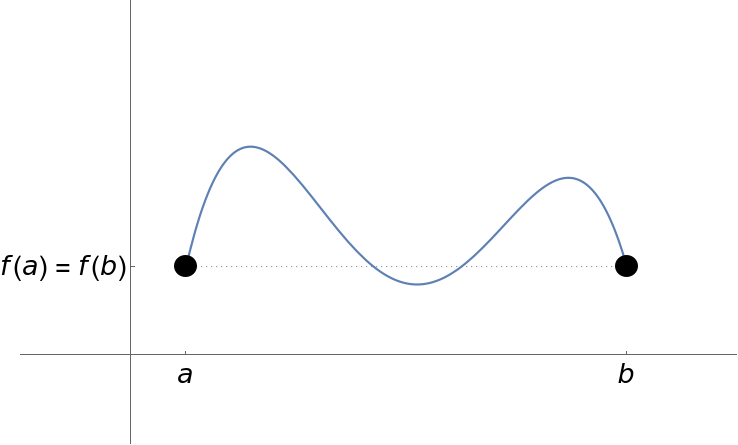
    You are using a browser not supported by the Wolfram Cloud

    Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


    I understand and wish to continue anyway »

    You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.