Detección de actas estadísticamente atípicas

Autor: Francisco Javier Rodríguez Arias
16 de junio de 2021 [Primera versión]​
18 de junio de 2021 [Actualización]

Introducción

En este artículo describiré y aplicaré una metodología para detectar actas que podríamos considerar estadísticamente atípicas. Esto se hará a dos niveles, a nivel de distrito y a nivel de local.

Teoría e hipótesis: distribución de votos en las actas

Distribución aleatoria de votos existentes

Demos por supuesto que ya tenemos la cantidad de votos para cada candidato, blancos y nulos. Estos valores serán fijos para cierta delimitación (sea provincia, distrito, local de votación). Es decir, comenzaremos asumiendo que tenemos en total  votos, y que en ese grupo hay  votos para el candidato 1,  votos para el candidato 2, ℬ votos blancos y  votos nulos (
=++ℬ+
). Entonces, si en un acta de votación se tienen  votos, escogeremos al azar de esa bolsa de  votos, compuesta de , , ℬ y  votos distintos, hasta llenar los  votos.
La distribución que se genera al escoger al azar de esa forma, se conoce como distribución hipergeométrica (y al ser más de 2 variables, sería la versión generalizada).
Aquí un breve ejemplo práctico de cómo se puede deducir:
Tengamos que  = 11,  = 10, ℬ = 1,  = 3, que daría  = 25.
Ahora tratemos de llenar un acta con  = 5 votos con esos datos. Digamos que será un acta con todos los votos para , ¿cuál es la probabilidad que esto ocurra? En primer lugar, la probabilidad de sacar una  de esa bolsa de 25, sería de 11/25, y luego, de volver a sacar otra sería 10/24, y así, dándonos:
In[]:=
11
25
10
24
9
23
8
22
7
21
Out[]=
1
115
Que en términos de factoriales se podría expresar como:
In[]:=
11!/6!
25!/20!
Out[]=
1
115
Y si dijéramos que hay 4  y 1 , entonces sería, 11/25 para sacar primero una , luego 10/24 para la segunda, 9/23 y 8/22 para la tercera y cuarta, y para la quinta, una , sería 10/21; pero también podría suceder que la  se saque primero, o segunda, o tercera o cuarta, entonces hay que considerar todos esos casos, y la probabilidad total será la suma de todos esos casos:
In[]:=
11
25
10
24
9
23
8
22
10
21
+
11
25
10
24
9
23
10
22
8
21
+
11
25
10
24
10
23
9
22
8
21
+
11
25
10
24
10
23
9
22
8
21
+
10
25
11
24
10
23
9
22
8
21
Out[]=
10
161
Esto es equivalente a:
In[]:=
11!/7!*10
25!/20!
*5
Out[]=
10
161
Ahora tratemos de llenar un acta con  = 5 votos de cualquier tipo. ¿De cuántas formas distintas se puede llenar? Podemos usar Permutations para tener una lista exhaustiva de las combinaciones posibles:
In[]:=
votos={,,,,,,,,,,,,,,,,,,,,,ℬ,,,};
In[]:=
Permutations[votos,{5}]//Short
Out[]//Short=
{{,,,,},{,,,,},{,,,,ℬ},{,,,,},{,,,,},{,,,,},{,,,,ℬ},618,{,,,,},{,,,,ℬ},{,,,,},{,,,,},{,,,,ℬ},{,,,ℬ,},{,,,ℬ,}}
In[]:=
%//Length
Out[]=
632
Hay entonces 632 formas (ordenadas) en que puedo llenar esos 5 votos. Pero como vimos antes, no todas estas combinaciones son igual de “probables”, pues cada  puede corresponder a un “votante” distinto.Entonces, tenemos que pensar cómo podemos escoger primero a los votantes. En general, si nos preguntáramos de cuántas formas puedo escoger 5 votantes de un grupo de 25, la respuesta sería:
In[]:=

25
5

Out[]=
53130
Entonces, ese sería nuestro denominador, y nuestro numerador para la probabilidad que estamos estimando serían los combinatorios de cada número de votos totales para una candidatura respecto a los votos escogidos. Que para el ejemplo que vimos con 4  y 1  sería el valor que ya calculamos anteriormente:
In[]:=

11
4

10
1


25
5

Out[]=
10
161
Si generalizamos la fórmula veríamos que la probabilidad de encontrar  votos para ,  para ,  para ℬ y  para  en  votos sería:
Out[]//TraditionalForm=
ℬ









ℬ+++

Y esa es la fórmula de probabilidad de una distribución hipergeométrica multivariada.

Simulación del caso práctico

Podemos poner a prueba en forma práctica también esta fórmula.
Generemos primero de forma aleatoria 1000 actas a partir de los "votos" propuestos en el ejemplo:
In[]:=
muestraAleatoria=Table[RandomSample[votos,5],1000];
Y contemos cuántos votos hay de cada uno en cada acta:
In[]:=
conteoPorActa=Lookup[Rule@@@Tally[#],{,,ℬ,},0]&/@muestraAleatoria;
In[]:=
conteoPorActa//Short
Out[]//Short=
{{3,2,0,0},{3,2,0,0},{2,2,1,0},{3,2,0,0},{2,2,0,1},{3,1,0,1},{0,3,1,1},{3,1,0,1},{1,4,0,0},{0,5,0,0},{1,3,0,1},978,{1,2,0,2},{3,1,1,0},{3,2,0,0},{3,1,0,1},{3,1,0,1},{2,1,1,1},{1,4,0,0},{1,3,0,1},{1,3,0,1},{0,5,0,0},{1,3,0,1}}
Y ahora podemos comparar la distribución marginal para cada variable:
In[]:=
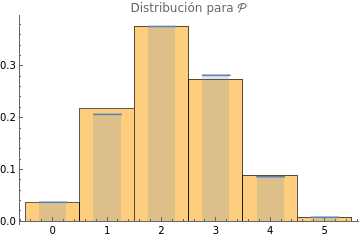
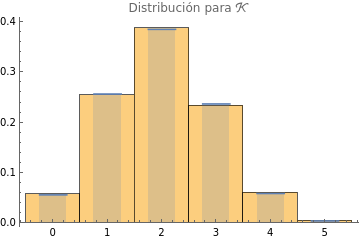
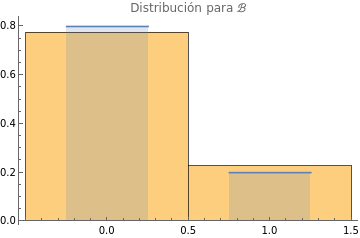
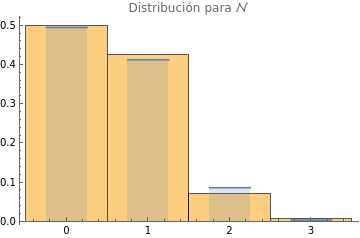
Table[Show[Histogram[conteoPorActa[[All,v]],{1},"ProbabilityDensity"],DiscretePlot[PDF[MarginalDistribution[MultivariateHypergeometricDistribution[5,{11,10,1,3}],v],i],{i,0,5},ExtentSizeScaled[1/2]],PlotLabel->Row[{"Distribución para ",{,,ℬ,}[[v]]}]],{v,4}]
Out[]=

,
,
,

Donde vemos que hay una buena coincidencia entre el histograma de la muestra aleatoria y la distribución teórica.
Ahora hagamos la misma simulación con 100000 actas, y veamos sus conteos y distribuciones:
In[]:=
muestraAleatoria=Table[RandomSample[votos,5],100000];
In[]:=
conteoPorActa=Lookup[Rule@@@Tally[#],{,,ℬ,},0]&/@muestraAleatoria;
In[]:=
conteoPorActa//Short
Out[]//Short=
{{3,1,0,1},{3,0,0,2},{2,2,1,0},{3,1,0,1},{2,1,1,1},{1,3,0,1},{1,2,1,1},{2,2,1,0},{2,2,0,1},{1,3,0,1},99980,{3,1,0,1},{2,2,0,1},{2,2,0,1},{3,1,0,1},{1,4,0,0},{1,2,1,1},{3,1,0,1},{2,3,0,0},{2,3,0,0},{1,3,0,1}}
In[]:=
Table[Show[Histogram[conteoPorActa[[All,v]],{1},"ProbabilityDensity"],DiscretePlot[PDF[MarginalDistribution[MultivariateHypergeometricDistribution[5,{11,10,1,3}],v],i],{i,0,5},ExtentSizeScaled[1/2]],PlotLabel->Row[{"Distribución para ",{,,ℬ,}[[v]]}]],{v,4}]
Out[]=

,
,
,

Donde vemos la convergencia de la coincidencia entre el histograma de la muestra aleatoria y la distribución teórica.

Distribución con grupos

Hay una consideración muy importante a considerar, y es que la agrupación de votantes en una mesa no es aleatoria. Las mesas están ordenadas por apellido dentro de un mismo local, lo cuál genera grupos y sesgos que no seguirían una muestra aleatoria como la analizada anteriormente.

Hipótesis nula

Para el propósito de este análisis usaremos como hipótesis que la distribución de votos dentro de cierta circunscripción puede seguir esta distribución hipergeométrica multivariada y analizaremos si es que se rechaza o no. Además, evaluaremos si al aplicarla se pueden identificar actas estadísticamente atípicas. Esta hipótesis asume implícitamente que los votantes dentro de esta circunscripción podrían haber estado aleatoriamente distribuidos en las mesas, por lo que no consideraremos el sesgo por el ordenamiento por apellido, el cual es indeterminable, hasta donde sabemos.

Sobre los datos

Código utilitario


Cargar datos

In[]:=
actasCompletas=Uncompress@CloudGet[CloudObject[
https://www.wolframcloud.com/obj/franciscoj/elecciones/2021-2/
actasCompletas
]];
La estructura de estos datos es una tabla que contiene en cada “fila” una lista con los siguientes datos: {“código de mesa”, “código de local”, “ubigeo”, “electores”, “votos”, “PL”, “FP”, “blancos”, “nulos”, “impugnados”, “observación 1”, “observación 2”}
In[]:=
TextGrid[RandomSample[actasCompletas,5],Frame->All]
Out[]=
012919
1242
060808
300
192
133
43
2
14
0
ACTA ELECTORAL NORMAL
CONTABILIZADAS NORMALES
045033
E063
140126
300
232
81
136
1
14
0
ACTA ELECTORAL NORMAL
CONTABILIZADAS NORMALES
034534
C762
140103
300
255
115
119
2
19
0
ACTA ELECTORAL NORMAL
CONTABILIZADAS NORMALES
017677
1667
080506
300
169
127
24
4
14
0
ACTA ELECTORAL NORMAL
CONTABILIZADAS NORMALES
077776
9989
240105
300
224
42
167
3
12
0
ACTA ELECTORAL NORMAL
CONTABILIZADAS NORMALES
Las observaciones son:
Y podemos comprobar cuál es el total de votos de todas las actas:
y verificar que corresponde exactamente a la publicación oficial de la ONPE al 100% en https://www.resultadossep.eleccionesgenerales2021.pe/SEP2021/EleccionesPresidenciales/RePres/T :

Filtrar por tipo

En este análisis solo consideraremos las actas electorales normales, que son las que no han pasado por el JEE. Cuando JEE resuelve un acta, puede cambiar los resultados por resolución, o anular el acta, así que nos enfocaremos solo en las actas que no han sido “modificadas” a posteriori. Las actas electorales normales son 84864.
Lista de actas normales:
Y la lista de actas que pasaron por JEE y fueron contabilizadas normalmente son 1397:

Estadísticas básicas

Veamos para cada grupo de actas las distribuciones de sus valores numéricos (electores, votos, votos para Perú Libre, para Fuerza Popular, blancos, nulos).

Histogramas de los datos numéricos de las actas normales (que no pasaron por los JEE)

Histogramas de los datos numéricos de las actas resueltas por el JEE y contabilizadas

Estadísticas por distrito

Analizaremos las estadísticas a nivel de cada distrito. En el Perú hay 1874 distritos, y además incluiremos como “distritos” los ubigeos usados por la ONPE en el extranjero, lo que suma 2082 ubigeos.
En cada distrito sacaremos los siguientes totales de las actas normales: electores, votos, votos a PL, FP, blancos, y nulos.
Veamos algunos casos extremos, para tener una visión de cómo se comportan diferentes distritos.
Distrito más grande:
Ese código de ubigeo corresponde a San Juan de Lurigancho, Lima.
Distrito con más votos a favor de Perú Libre:
Ese código de ubigeo corresponde a Juliaca, San Ramón, Puno.
Distrito con más votos a favor de Fuerza Popular:
Ese código de ubigeo corresponde a Santiago de Surco, Lima.
Distrito de más de 50000 electores con menor diferencia absoluta entre ambos:
Ese código de ubigeo corresponde a Lambayeque, Lambayeque, Lambayeque.
Se puede ver el detalle de cómo se comportan los votos de estos distritos en la sección Anexo, Estadísticas de votos en distritos extremos.

Cálculos y resultados

Simulación y prueba de ajuste a la distribución de la hipótesis nula

A nivel distrital

La distribución hipergeométrica multivariada tiene el problema de solo ser aplicable a un número fijo de elementos. Entonces, para poder rechazar o no la hipótesis, generaremos en forma aleatoria para cada mesa una muestra de la distribución propuesta y se combinarán esas muestras para cada distrito. Usaremos 1000 distribuciones para cada acta. Esto significa que para cada distrito simularemos 1000 escenarios usando la distribución propuesta.
Resumen:
Porcentaje de distritos con información suficiente donde es no se rechaza la hipótesis:

A nivel de local de votación

Haremos el mismo ejercicio a nivel de local de votación.
Resumen:
Porcentaje de locales con información suficiente donde es no se rechaza la hipótesis:

Evaluación de actas atípicas

Dado que a nivel de distritos y de locales hay muchos casos donde la hipótesis de la distribución no se rechaza, asignaremos el valor de probabilidad de acta a cada una usando la distribución hipergeométrica multivariada. Esto lo haremos sobre todas las actas, pero separaremos los resultados de los casos donde la distribución se rechazó de los que no.

A nivel distrital

Saquemos la lista plana de actas:
¿Qué valores de probabilidades hay?
Casos atípicos para distritos en los que no se rechaza la hipótesis de la distribución
Filtraremos las actas que corresponden a ubigeos en los que no se rechazó la hipótesis y que además tengan más de 0 votos.
Separemos las actas atípicas:
Y estos serían los totales para las actas rechazadas:
Veamos algunos de los casos con menor probabilidad:
En esos casos se puede ver que lo que hizo que tuvieran menor probabilidad es la gran cantidad de nulos.
¿En cuántas actas de las rechazadas había 0 votos para Perú Libre?
¿En cuántas actas de las rechazadas había 0 votos para Fuerza Popular?
Pero cuántas actas que no fueron catalogadas como atípicas tenían 0 votos para cada candidato:
Para Perú Libre:
Para Fuerza Popular:
Es decir, en las actas donde la hipótesis no se rechazó, para las actas con 0 votos para Perú Libre, los 7 casos pasan como actas típicas, y en los casos de 0 votos para Fuerza Popular, 9 casos son atípicos y 21 casos son plausibles. Entonces que un acta tenga 0 votos para un candidato no significa que sea atípica.
Veamos qué actas tenían 0 votos y se consideraron atípicas :
Veamos qué actas tenían 0 votos pero se consideraron típicas:
Casos atípicos para distritos en los que se rechaza la hipótesis de la distribución
Filtraremos las actas que corresponden a ubigeos en los que se rechazó la hipótesis y que además tengan más de 0 votos.
Separemos las actas atípicas:
Son muchas más actas “atípicas” que en el caso anterior, y esto es porque en realidad sabemos que en esos distritos la distribución hipergeométrica multivariada no es válida. Igualmente revisaremos estos casos, pero con la importante advertencia que no son significativos.
Y estos serían los totales para las actas rechazadas:
Veamos algunos de los casos con menor probabilidad:
Igual que en los casos anteriores, en este grupo también son las actas con exceso de nulos las más atípicas.
¿En cuántas actas de las rechazadas había 0 votos para Perú Libre?
¿En cuántas actas de las rechazadas había 0 votos para Fuerza Popular?
Pero cuántas actas que no fueron catalogadas como atípicas tenían 0 votos para cada candidato:
Para Perú Libre:
Para Fuerza Popular:
Es decir, en las actas donde la hipótesis se rechazó, no hay actas con 0 votos para Perú Libre, y en los casos de 0 votos para Fuerza Popular, 18 casos son atípicos y 21 casos son plausibles.
Veamos qué actas tenían 0 votos y se consideraron atípicas :
Veamos qué actas tenían 0 votos pero se consideraron típicas :
Casos atípicos para distritos en los que no hay información
Filtraremos las actas que corresponden a ubigeos en los que no había suficiente información y que además tengan más de 0 votos.
Separemos las actas atípicas:
En general al ser distritos con muy poca información, la mayoría de actas se considerarían de probabilidad “alta” pues la muestra de base no es significativa.
Y estos serían los totales para las actas rechazadas:
Veamos algunos de los casos con menor probabilidad:
En este caso, ninguna de las actas “atípicas” tiene 0 votos para ninguno de los candidatos.
Pero cuántas actas que no fueron catalogadas como atípicas tenían 0 votos para cada candidato:
Para Perú Libre:
Para Fuerza Popular:
Hay 7 actas con 0 votos para Perú Libre, y 0 actas con 0 votos para Fuerza Popular.
Veamos qué actas tenían 0 votos pero se consideraron típicas :
Obviamente los casos con 1 de probabilidad significa que solo había un acta, así que no tienen punto de comparación.

A nivel de local

Saquemos la lista plana de actas:
¿Qué valores de probabilidades hay?
Casos atípicos para locales en los que no se rechaza la hipótesis de la distribución
Filtraremos las actas que corresponden a locales en los que no se rechazó la hipótesis y que además tengan más de 0 votos.
Como se puede ver, a nivel de local una gran mayoría de actas no rechaza la hipótesis nula.
Separemos las actas atípicas:
Y estos serían los totales para las actas rechazadas:
Veamos algunos de los casos con menor probabilidad:
En esos casos se puede ver que lo que hizo que tuvieran menor probabilidad es la gran cantidad de nulos.
¿En cuántas actas de las rechazadas había 0 votos para Perú Libre?
¿En cuántas actas de las rechazadas había 0 votos para Fuerza Popular?
Pero cuántas actas que no fueron catalogadas como atípicas tenían 0 votos para cada candidato:
Para Perú Libre:
Para Fuerza Popular:
Es decir, en las actas donde la hipótesis no se rechazó, para las actas con 0 votos para Perú Libre, los 7 casos pasan como actas típicas, y en los casos de 0 votos para Fuerza Popular, 11 casos son atípicos y 30 casos son plausibles. Entonces que un acta tenga 0 votos para un candidato no significa que sea atípica.
Veamos qué actas tenían 0 votos y se consideraron atípicas :
Veamos qué actas tenían 0 votos pero se consideraron típicas :
Casos atípicos para locales en los que se rechaza la hipótesis de la distribución
Filtraremos las actas que corresponden a locales en los que se rechazó la hipótesis y que además tengan más de 0 votos.
Separemos las actas atípicas:
Es interesante que en este caso sean mucho menos los casos atípicos que en los casos en los que no se rechazó la hipótesis.
Y estos serían los totales para las actas rechazadas:
Veamos algunos de los casos con menor probabilidad:
Igual que en los casos anteriores, en este grupo también son las actas con exceso de nulos las más atípicas.
¿En cuántas actas de las rechazadas había 0 votos para Perú Libre?
¿En cuántas actas de las rechazadas había 0 votos para Fuerza Popular?
Pero cuántas actas que no fueron catalogadas como atípicas tenían 0 votos para cada candidato:
Para Perú Libre:
Para Fuerza Popular:
Es decir, en las actas donde la hipótesis nula se rechazó, no hay actas con 0 votos para Perú Libre, y en los casos de 0 votos para Fuerza Popular, 1 caso es atípico y 4 casos son plausibles.
Veamos qué actas tenían 0 votos y se consideraron atípicas :
Veamos qué actas tenían 0 votos pero se consideraron típicas :
Casos atípicos para distritos en los que no hay información
Filtraremos las actas que corresponden a locales en los que no había suficiente información y que además tengan más de 0 votos.
Separemos las actas atípicas:
Es interesante ver que hay bastantes actas con baja probabilidad a pesar de estar en locales con poca información.
Y estos serían los totales para las actas rechazadas:
Veamos algunos de los casos con menor probabilidad:
En este caso, ninguna de las actas “atípicas” tiene 0 votos para ninguno de los candidatos, y además en todas hay un número inusual de nulos.
¿Cuántas actas atípicas tienen 0 votos para un candidato?
Para Perú Libre:
Para Fuerza Popular:
Pero cuántas actas que no fueron catalogadas como atípicas tenían 0 votos para cada candidato:
Para Perú Libre:
Para Fuerza Popular:
Es decir, hay 3 actas atípicas con 0 votos para Fuerza Popular y 7 actas con 0 votos para Perú Libre son plausibles, así como 20 actas con 0 votos para Fuerza Popular.
Veamos qué actas tenían 0 votos pero se consideraron atípicas :
Veamos qué actas tenían 0 votos pero se consideraron típicas :
Obviamente los casos con 1 de probabilidad significa que solo había un acta, así que no tienen punto de comparación para generar una información relevante.

Combinando nivel distrital y de locales

Enfoquémonos solo en los casos en los que no se rechazó la hipótesis nula. ¿Cuántas actas fueron catalogadas como atípicas por ambos niveles? ¿Cuántas en uno solo?
Votos correspondiente a las actas atípicas a nivel distrital y de local
Votos correspondiente a las actas atípicas a nivel distrital pero no de local
Votos correspondiente a las actas atípicas a nivel de local pero no distrital
Votos correspondiente a las actas atípicas a nivel distrital o de local

Evaluación de actas atípicas en las enviadas al JEE

Para calcular la probabilidad de las actas enviadas al JEE usaremos la distribución de las actas normales, tanto a nivel distrital como de local.

A nivel distrital

Saquemos la lista plana de actas:
Casos en los que no se puede determinar ninguna probabilidad:
Casos atípicos para distritos en los que no se rechaza la hipótesis
Filtraremos las actas que corresponden a ubigeos en los que no se rechazó la hipótesis y que además tengan más de 0 votos y una probabilidad válida.
Separemos las actas atípicas:
Y estos serían los totales para las actas rechazadas:
Podemos ver la lista completa de actas atípicas:

A nivel de local

Saquemos la lista plana de actas:
Casos en los que no se puede determinar ninguna probabilidad:
Casos atípicos para locales en los que no se rechaza la hipótesis
Filtraremos las actas que corresponden a ubigeos en los que no se rechazó la hipótesis y que además tengan más de 0 votos y una probabilidad numérica.
Separemos las actas atípicas:
Y estos serían los totales para las actas rechazadas:
Podemos ver la lista completa de actas atípicas:
Veamos algunos ejemplos de estas actas atípicas:

Resumen y distribución geográfica de actas atípicas

Si consideramos solo las actas atípicas correctamente identificadas podemos hacer el siguiente resumen:

Estadísticas por región

Si consideramos solo las actas atípicas correctamente identificadas podemos hacer los siguientes resúmenes a distintos niveles:
tabla a nivel distrital
tabla a nivel de locales
tabla combinada

Visualización geográfica

Conclusiones

La primera conclusión de nuestro análisis es que sí se puede verificar que en algunos distritos y en algunos locales se puede usar una distribución estadística como la hipergeométrica multivariada para detectar actas que se puedan considerar estadísticamente atípicas y que la verosimilitud de esta distribución a nivel de locales es mejor que a nivel distrital. Que sean atípicas no significa que sean imposibles, solo que son menos probables respecto a la distribución escogida. Una consideración importante respecto a las actas atípicas es que los votantes de un local se ordenan alfabéticamente según el apellido y se dividen en mesas que agrupan el mismo apellido usualmente, lo que genera grupos artificiales con respecto al resto de mesas. Esto hace que los resultados a nivel de mesa parezcan sesgados respecto a un promedio más general y que las desviaciones sean más plausibles.
Otra conclusión importante es cómo cambiaría la diferencia de votos si quitáramos del conteo las actas atípicas según el nivel de detección que se escoja. Considerando solo las actas contabilizadas sin observación o resolución alguna, y si quitáramos usando solo las detectadas a nivel de distrito, Perú Libre disminuiría en 82733 votos y Fuerza Popular en 52994, lo que significaría acortar la distancia con la que ha ganado Perú Libre de 44058 votos a solo 14319 (recordemos que a este nivel solo se toma en cuenta el 78,2% de distritos con información suficiente). Si se hiciera solo a nivel de locales a Perú Libre se le restarían 138418 votos y a Fuerza Popular 141995, lo que incrementaría ligeramente la diferencia con la que gana Perú Libre a 47635 votos (a este nivel se cubre el 96,7% de locales con información suficiente). Si se usaran ambos criterios, Perú Libre disminuiría en 184800 votos y Fuerza Popular en 173017, lo que acortaría un poco la diferencia entre ambos candidatos, a 32275 votos.
Los casos de las actas que pasaron por el JEE y resultaron siendo catalogadas como atípicas simplemente muestran actas cuya resolución generó un acta muy poco probable ya que, en muchos casos, al resolver un acta se mandaron los votos de un partido a 0 y se aumentaron en forma artificial los nulos. No se puede determinar que haya un sesgo en esta anulación de votos que pudiera afectar el resultado final.

Anexo

Estadísticas de votos en distritos extremos

San Juan de Lurigancho, Lima

Por ejemplo, para San Juan de Lurigancho (el distrito con más electores) tenemos el siguiente resultado:
Podemos también ver las distribuciones de votos para ese distrito:

Juliaca, San Román, Puno

Veamos ahora Juliaca, San Román, Puno, el distrito con mayor diferencia de votos a favor de Perú Libre:
Podemos también ver las distribuciones de votos para ese distrito:

Santiago de Surco, Lima

Veamos ahora Santiago de Surco, Lima, el distrito con mayor diferencia de votos a favor de Fuerza Popular:
Podemos también ver las distribuciones de votos para ese distrito:

Lambayeque, Lambayeque, Lambayeque

Veamos ahora el distrito de Lambayeque en Lambayeque, que es el distrito (grande) con menor diferencia de votos entre Perú Libre y Fuerza Popular:
Hay una ligera ventaja de Fuerza Popular:
Podemos también ver las distribuciones de votos para ese distrito: