Wolfram|Alpha Notebook Edition for Wolfram|Alpha Users
Wolfram|Alpha Notebook Edition for Wolfram|Alpha Users
Combined Presentation Notebooks from Oct 7th Outreach Livestream with Noah Chartoff and John McNally
For Those Familiar with Wolfram|Alpha
And a slight bias toward educators.
Wolfram|Alpha places you have hopefully visited
Wolfram|Alpha places you have hopefully visited
The homepage, with natural language or traditional math inputs:
https://www.wolframalpha.com/
Examples by topic, in case you aren’t sure what you want yet:
https://www.wolframalpha.com/examples
A problem generator for practicing skills:
https://www.wolframalpha.com/problem-generator/
https://www.wolframalpha.com/
Examples by topic, in case you aren’t sure what you want yet:
https://www.wolframalpha.com/examples
A problem generator for practicing skills:
https://www.wolframalpha.com/problem-generator/
Use the natural language tools you love from Wolfram|Alpha in Wolfram|Alpha Notebook Edition
Use the natural language tools you love from Wolfram|Alpha in Wolfram|Alpha Notebook Edition
You can use natural language inputs you are used to from Wolfram|Alpha. There are a variety of calculation tools as well as access to the knowledge base through natural language inputs.
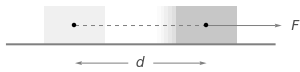
Calculation Tool Example for the Physical Sciences
Calculation Tool Example for the Physical Sciences
In[2]:=
FormulaData[{"Work", "Standard"}]
Out[2]=
W
d
F
This will look familiar to you if you have used this feature of Wolfram|Alpha. The input below is obtained by using the “full Wolfram|Alpha results” button after you enter a natural language input
In[3]:=
mechanicalworkcalculator
Calculation Tool Example for Mathematics
Calculation Tool Example for Mathematics
In[4]:=
Out[4]=
146.88
You can also just say what you want to do as a specific sum instead of using a general-purpose calculator.
In[5]:=
Out[5]=
Easily add or remove extra details in the natural language query to adjust those parameters.
In[6]:=
Out[6]=
Not Just for Science and Math!
Not Just for Science and Math!
There are computable datasets for areas of study outside traditional “STEM” fields. Your imagination is your limit for how to use this curated data in lessons.
The next input generates an EntityClass, which can be made into an EntityList in the following line. These are built-in symbols in the Wolfram Language, and can be used in all the usual ways by those familiar with these constructs.
The previous output defines a category of things by the specified criterion. It can be displayed as a concrete list as well. Notice that knowledge of exact syntax was not needed to generate the list below, only a little conceptual knowledge was needed go from the last natural language input to this one.
Remember that you can browse for examples at https://www.wolframalpha.com/examples if you want inspiration for what topics have lots of available data to use in your lessons.
Where to Start with the Differences?
Where to Start with the Differences?
Starting Points!
Starting Points!
Browse form a long list of subject areas that can provide inspiration, act as tutorial, or sometimes even solve the exact problem you were looking for. These can be found in the orange navigation bar at the top of a Wolfram|Alpha-Mode Notebook, right between Browse Demonstrations and Browse Interactive Plot Quizzes.
Quizzes to Browse or Start with Natural Language Input
Quizzes to Browse or Start with Natural Language Input
Demonstrations
Demonstrations
In the orange navigation bar at the top of a Wolfram|Alpha-Mode Notebook, try the Browse Demonstrations button and look around. For example:
Browse Demonstrations >> US Common Core >> High School: Statistics & Probability >>
Using Probability to Make Decisions >> HSS-MD.A.3 >> Dice Roller & Penny Flipper
Browse Demonstrations >> US Common Core >> High School: Statistics & Probability >>
Using Probability to Make Decisions >> HSS-MD.A.3 >> Dice Roller & Penny Flipper
Inputs and Outputs
Inputs and Outputs
Wolfram|Alpha
Wolfram|Alpha
Wolfram|Alpha gives what you asked for, as well as additional relevant information you might be looking for.
Very handy if you aren’t quite sure what else you might need or if you forgot you needed something until you see it.
Wolfram|Alpha Notebook Edition
Wolfram|Alpha Notebook Edition
Wolfram|Alpha Notebook edition produces a specific, computable object as an output line for any input. It also shows what Wolfram Language code produced that output line.
Wolfram|Alpha Notebook Edition outputs are cells in a notebook. This means that they are computable objects that can be used and manipulated just like any Wolfram Language output. Try changing the viewing angle of the 3D graphics above by clicking and holding the mouse over the output above.
You don’t need to choose! With Wolfram|Alpha Notebook Edition, you can have both.
You don’t need to choose! With Wolfram|Alpha Notebook Edition, you can have both.
If you are using Wolfram|Alpha Notebook Edition and decide you do want to see the full Wolfram|Alpha results, you can with the click of a button. Just use the “full Wolfram|Alpha results” button that appears after you enter a natural language input.
Below are the “full Wolfram|Alpha results” for the last input.
Sequential Computations in a Notebook
Sequential Computations in a Notebook
Great for following a train of thought computationally, just like any Wolfram Notebook!
Great for following a train of thought computationally, just like any Wolfram Notebook!
In this example, students can trade a “formula sheet” (which isn’t really much help unless you already know where to look) for an interactive interface that allows them to think about exactly which information they need to solve a problem.
Use the result to define a function for future use.
Derive another common formula using what you’ve already defined.
Now your students have to think about why there really are 3 answers to their last input. Do they remember what they learned about solutions to cubic polynomials in one variable? There will in general be 3 complex solutions to a cubic polynomial, so you can instead ask for only solutions over the reals.
Just like any Wolfram Language workflow, there is more than one way to express an idea
Just like any Wolfram Language workflow, there is more than one way to express an idea
These two inputs replicate what was done above, but a second student will likely decide to phrase the natural language inputs differently from the first. The results will be the same!
Refer to previous lines and previously defined functions
Refer to previous lines and previously defined functions
Now your student may want to explore the relationship between surface area and volume in the context of some problem.
Refer to the previously defined function for an easy flow of computational thought in natural language.
Your student can also visualize results with natural language. This will help them explore patterns in your lessons.
Use Manipulate to Explore Structure
Use Manipulate to Explore Structure
Understanding the geometry related to algebraic expressions is a key learning goal
Understanding the geometry related to algebraic expressions is a key learning goal
Start off with a simple line. You can adjust the vertical range, horizontal range, or any of the parameters you specify by using the sliders below the plot.
Extend to higher degree polynomials. By hands-on-exploration, your students will get an intuition for how parameters in an algebraic expression change the geometry of its graph.
In sum, Wolfram|Alpha users will feel right at home in Wolfram|Alpha Notebook Edidtion
In sum, Wolfram|Alpha users will feel right at home in Wolfram|Alpha Notebook Edidtion
Familiar natural language tools with some nice twists.
If you are familiar with the Wolfram Language, you can use all your knowledge in Wolfram|Alpha Notebook Edition too!
This is the topic of the next chapter.
If you are familiar with the Wolfram Language, you can use all your knowledge in Wolfram|Alpha Notebook Edition too!
This is the topic of the next chapter.
Wolfram|Alpha Notebook Edition: an introduction for Wolfram Language veterans
Natural Language is naturally great
Natural Language is naturally great
For new users, Wolfram|Alpha Notebook Edition is a great tool, usable with even minimal instruction.
Wolfram’s NaturalLanguage will permit us to do a lot of great work without actually knowing the Wolfram Language. Even complicated calculations can be done easily, with lots of available “step by step” explanations.
Natural language lets us flexibly define multiple variables or functions.
Wolfram’s NaturalLanguage will permit us to do a lot of great work without actually knowing the Wolfram Language. Even complicated calculations can be done easily, with lots of available “step by step” explanations.
Natural language lets us flexibly define multiple variables or functions.
By default, if you click an empty cell (or between existing cells) and start typing in Mathematica, you’ll get an “input cell,” that you can use to create Wolfram Code, like this:
But in Wolfram|Alpha Notebook Edition, the default cell type is a “free-form input cell”, like this:
You can write any instructions in these orange cells (e.g. 2+2) and activate these cells by clicking inside them and hitting the enter key. (You can try that out with the above orange cell if you want: I haven’t activated it yet).
NOTE: In Mathematica, you’d need to hit shift and enter. In a Natural Language Input cell, that will add a second line to the code instead of running it. We’ll discuss the role of this second line further on.
These free-form cells (also called “natural language cells”) let us flexibly use the functionality of Mathematica, without having to worry about the exact syntax of our code or query. It will take any instructions written in English, and translate it (using Wolfram|Alpha) into correctly formatted Wolfram Language code! This combines the power of Mathematica with the ease-of-use of Wolfram Alpha.
As an example, let’s define multiple functions, using the sort of language we might use when speaking.
NOTE: In Mathematica, you’d need to hit shift and enter. In a Natural Language Input cell, that will add a second line to the code instead of running it. We’ll discuss the role of this second line further on.
These free-form cells (also called “natural language cells”) let us flexibly use the functionality of Mathematica, without having to worry about the exact syntax of our code or query. It will take any instructions written in English, and translate it (using Wolfram|Alpha) into correctly formatted Wolfram Language code! This combines the power of Mathematica with the ease-of-use of Wolfram Alpha.
As an example, let’s define multiple functions, using the sort of language we might use when speaking.
Each of the definitions above use a different syntax (sometimes I used brackets, sometimes parentheses, and I wrote different English words in each time), but they are all translated as the correct code that defines a function.
These definitions stay until they are cleared, and can be used arithmetically, or to define other new functions.
These definitions stay until they are cleared, and can be used arithmetically, or to define other new functions.
It even includes an example of the actual Wolfram Language code it generated, when applicable.
It even includes an example of the actual Wolfram Language code it generated, when applicable.
And typically, (most) formal code that works in Mathematica’s input cells will also work in a natural language cell.
You can see that the code in the orange cell above and the code in the input cell right below it are identical: Wolfram|Alpha Notebook Edition didn’t need to translate anything because the code was already correctly written in the Wolfram Language. Just for fun, let’s see if the program can write the above code from a more informal prompt:
It worked! The two outputs above aren’t exactly the same (for example, the starting values and ranges of “a” are different), but that’s something we can change. The code Wolfram|Alpha Notebook Edition produces is editable. If you click on the input cell above (the cell with formal code generated right below the orange cell), you can change the produced code however you want (for example, you could change the range of “a” from 0, 2 to 1, 5 ) then hit Shift+Enter to run the new instructions. This lets newer users generate their own formal code with informal commands, and then explore what changing that code will do.
We’ll return to the editable nature of this code later, and see how it could help us more than just by refining our results. For now, we’ll just note that the provided code after a Natural Language input cell is run could be used to either help students do math without learning any code or could scaffold the learning of the Wolfram Language, starting with “no-code” Natural Language prompts. However you want to teach your students, this program has something that will help.
However, there is some code that works in “standard inputs” (i.e. Inputs in Mathematica) that doesn’t work as well in Natural Language. To see what makes this happens (and how we can avoid it), we’ll move on to an example.
We’ll return to the editable nature of this code later, and see how it could help us more than just by refining our results. For now, we’ll just note that the provided code after a Natural Language input cell is run could be used to either help students do math without learning any code or could scaffold the learning of the Wolfram Language, starting with “no-code” Natural Language prompts. However you want to teach your students, this program has something that will help.
However, there is some code that works in “standard inputs” (i.e. Inputs in Mathematica) that doesn’t work as well in Natural Language. To see what makes this happens (and how we can avoid it), we’ll move on to an example.
Mathematica and Wolfram|Alpha Notebook Edition are different
Mathematica and Wolfram|Alpha Notebook Edition are different
Mathematica is a bit more customizable than Wolfram|Alpha Notebook Edition.
WANE doesn’t have a slideshow pallet, and can’t accept different “style-sheets” to change the default look
There is some code that works in standard inputs that doesn’t work well in Natural Language
(At least at first. We’ll discuss how to fix these problems).
Notice that the code interpreted the line break above as a blank space, which in Mathematica code is equivalent to multiplication. So it ended up multiplying the 3 and 4 together, rather than just giving us two sums (5 and 10).
You can see the “blank” multiplication more clearly below:
You can see the “blank” multiplication more clearly below:
And when we try to use more complicated examples, the multiplication can still creep in.
You can see how the blank space above works similarly, trying to multiply the 3 and 3x together.
This is done because the program assumes that users of Wolfram|Alpha Notebook Edition are new to coding, and thus won't try anything too complicated within a single cell. But when a veteran of the Wolfram Language approaches the program, it can cause some friction (in the next section, we'll talk about how to prevent this kind of problem altogether).
An easy way to fix the multi line issue is to break the code into separate cells:
This is done because the program assumes that users of Wolfram|Alpha Notebook Edition are new to coding, and thus won't try anything too complicated within a single cell. But when a veteran of the Wolfram Language approaches the program, it can cause some friction (in the next section, we'll talk about how to prevent this kind of problem altogether).
An easy way to fix the multi line issue is to break the code into separate cells:
Unfortunately, there’s a larger issue. Let’s see what happens when we take just the first “line” of code from your original command.
It didn’t work! The error message gives us a hint as to why: it says “No Wolfram Language translation found.” The program has attempted to translate this into code, and isn’t sure how to do it.
Of course, we don’t want a translation to happen at all: the code is already exactly the way we want it. The unfortunate fact is that the Natural Language cell doesn’t know that. I’ll explain why.
Wolfram|Alpha Notebook Edition will try to translate your English instructions into mathematical code. Unfortunately, it sometimes can’t tell the difference between the two because many common letters are used as defined variables in various fields of study. Let’s look at what happens when we just input the command “g1”:
Of course, we don’t want a translation to happen at all: the code is already exactly the way we want it. The unfortunate fact is that the Natural Language cell doesn’t know that. I’ll explain why.
Wolfram|Alpha Notebook Edition will try to translate your English instructions into mathematical code. Unfortunately, it sometimes can’t tell the difference between the two because many common letters are used as defined variables in various fields of study. Let’s look at what happens when we just input the command “g1”:
In[47]:=
g1
Unfortunately, “g1” already has a defined meaning. It’s the g note three scales down from middle c (incidentally, g2 is the note one scale above it). The program thus became confused as to whether we were trying to define a function or get information about a musical note, or what. This becomes even more complicated because g has different meanings in a lot of scientific fields (g1 could be gene, or 1 gram, or the gravitational constant times 1).
Wolfram|Alpha Notebook Edition is working on this issue! Some examples that didn’t work even a month ago work now. But for the moment, it’s still a potential problem that could cause errors in code that works perfectly well in Mathematica.
But there are solutions!
Wolfram|Alpha Notebook Edition is working on this issue! Some examples that didn’t work even a month ago work now. But for the moment, it’s still a potential problem that could cause errors in code that works perfectly well in Mathematica.
But there are solutions!
So how do we use Wolfram Language syntax in Wolfram|Alpha Notebook Edition?
So how do we use Wolfram Language syntax in Wolfram|Alpha Notebook Edition?
There’s more than one approach to fixing this. First, I’ll talk about some ways that your students might naively stumble upon. But then I’ll pitch the best option for an experienced user like yourself: using the usual Input format you find in Mathematica.
One (unideal) way to approach this problem is to define new terms with language that has no inherent meaning. For example, note that capital X and capital Y have no set meanings in Wolfram Alpha:
One (unideal) way to approach this problem is to define new terms with language that has no inherent meaning. For example, note that capital X and capital Y have no set meanings in Wolfram Alpha:
So they are viable candidates for redefining.
Although this works, it’s unideal. We are very proud of our backwards compatibility at Wolfram: code that worked in previous versions of Mathematica will always work in newer versions of Mathematica (unless it relies on a third-party software like flash).
And some great Wolfram resources (like the Wolfram Demonstrations project) use older code. And non Wolfram resources, like Stack Exchange, give Wolfram Language code examples that could be very useful. So we want a solution that lets us use this backwards compatibility without changing the code at all.
The good news is we can use this code precisely as it was originally written. We’ll just need to use a regular Input cell, like we would find in Mathematica.
There’s multiple ways to create one of these (probably the easiest is to use a Natural Language cell to do a simple calculation, like 2+3, then edit the input cell that appears below it).
To talk about why this works, let’s return to the previous 3D example above.
You could also copy the input cell, then paste it elsewhere and put whatever code you want in it.
And some great Wolfram resources (like the Wolfram Demonstrations project) use older code. And non Wolfram resources, like Stack Exchange, give Wolfram Language code examples that could be very useful. So we want a solution that lets us use this backwards compatibility without changing the code at all.
The good news is we can use this code precisely as it was originally written. We’ll just need to use a regular Input cell, like we would find in Mathematica.
There’s multiple ways to create one of these (probably the easiest is to use a Natural Language cell to do a simple calculation, like 2+3, then edit the input cell that appears below it).
To talk about why this works, let’s return to the previous 3D example above.
You could also copy the input cell, then paste it elsewhere and put whatever code you want in it.
But a cleaner way (that doesn’t generate a superfluous Natural Language cell) is to do the following:
Click on an empty space (where the cursor turns sideways)
Click on the plus sign that appears on the left of the screen
Select "Other Style of Text..."
Click on the word next to the instructions “Select or type a style name” and type the name Input
NOTE: The option for “input” won’t appear in the drop down menu. But this will still create such a cell
Having done this, you’ll create a normal input cell that you can use your original code in:
You have now created a normal Input cell that can take any code that runs in Mathematica (that doesn’t include Parallelization) and run it! This sidesteps the translation issue entirely.
Also note: now that you’ve defined g1 and g2 in this notebook, you can use them in Natural Language cells and they will (usually) understand what you mean.
Also note: now that you’ve defined g1 and g2 in this notebook, you can use them in Natural Language cells and they will (usually) understand what you mean.
It’s also worth noting that documents created in Mathematica will work if you open them with Wolfram|Alpha Notebook Edition. So your older worksheets or readings will definitely still work with this new program.
It’s worth noting that improvements are being made in this translation system every day! I had to rewrite this notebook from a previous example, because code that previously didn’t work in Natural Language cells now do! Here’s another example:
Wolfram|Alpha notebook edition used to return errors when running parallelized code. I used the below example in previous talks, showing that although the code returned error messages when it tried to factor several numbers at once (using more than one kernel for simultaneous calculations), it was able to factor these numbers sequentially after those errors, and thus got the desired job done. But now parallelization appears to be possible in Wolfram|Alpha Notebook Edition! You can see the previous errors below, but if you run the code yourself now the error messages should go away as the program processes the code in parallel.
It’s worth noting that improvements are being made in this translation system every day! I had to rewrite this notebook from a previous example, because code that previously didn’t work in Natural Language cells now do! Here’s another example:
Wolfram|Alpha notebook edition used to return errors when running parallelized code. I used the below example in previous talks, showing that although the code returned error messages when it tried to factor several numbers at once (using more than one kernel for simultaneous calculations), it was able to factor these numbers sequentially after those errors, and thus got the desired job done. But now parallelization appears to be possible in Wolfram|Alpha Notebook Edition! You can see the previous errors below, but if you run the code yourself now the error messages should go away as the program processes the code in parallel.
The bottom line:
The bottom line:
Wolfram|Alpha Notebook Edition is an excellent tool for new users. It can cut down on the time needed to learn precise syntax and let students focus on exploring the mathematics.
Ironically, that sometimes means that experienced user of Mathematica run into something in Wolfram|Alpha Notebook Edition which runs counter to their experience. You experienced one of them now. But with some investigation, the best way to run Wolfram Language code in a natural language cell can be found.
If you’re a Wolfram Language veteran, this tool may get some getting used to. But once you’ve had some time to explore it I think you’ll find it’s a valuable resource for novices and experts alike.
Ironically, that sometimes means that experienced user of Mathematica run into something in Wolfram|Alpha Notebook Edition which runs counter to their experience. You experienced one of them now. But with some investigation, the best way to run Wolfram Language code in a natural language cell can be found.
If you’re a Wolfram Language veteran, this tool may get some getting used to. But once you’ve had some time to explore it I think you’ll find it’s a valuable resource for novices and experts alike.
Bonus Topic: Using Wolfram|Alpha Notebook Edition to Drive Critical Thinking in Lessons
Wolfram|Alpha Notebook Edition Allows Focus on Strategic Problem Solving
(Rather than computation details)
Wolfram|Alpha Notebook Edition Allows Focus on Strategic Problem Solving
(Rather than computation details)
(Rather than computation details)
Allow your students to learn how to parse a complex situation (or wall of text) into a strategic plan for solving a problem. This is a distinct skill from the calculation details. While many modes of teaching don’t let you disentangle the strategic thinking from the calculation details, natural language computation lets you focus on exactly the skill you want to teach!
An example from a former colleague’s homework
An example from a former colleague’s homework
Suppose a 1.00 kg mass experiences an acceleration of 7.00 m/s^2 at 20.0 degrees with respect to the positive x axis.
A.) What are the components of the net force acting on the mass in the standard Cartesian basis?
B.) If the net force is the resultant of two forces, and one is 4.00 Newtons at -30.0 degrees with respect to the positive x axis, what are the components of the second force in the standard Cartesian basis?
C.) What is the second force given in polar form?
A.) What are the components of the net force acting on the mass in the standard Cartesian basis?
B.) If the net force is the resultant of two forces, and one is 4.00 Newtons at -30.0 degrees with respect to the positive x axis, what are the components of the second force in the standard Cartesian basis?
C.) What is the second force given in polar form?
tl;dr (parsing this wall of text into strategic goals to solve the problem)
tl;dr (parsing this wall of text into strategic goals to solve the problem)
1.) use Newton’s Second Law
2.) convert between coordinate systems
3.) do some vector arithmetic
4.) convert back to the old coordinate system
2.) convert between coordinate systems
3.) do some vector arithmetic
4.) convert back to the old coordinate system
Strategic Goal 1 - Turn the given quantities into a net force
Strategic Goal 1 - Turn the given quantities into a net force
Another pathway to the same place in case your students forget that “Newtons” are a derived unit.
Strategic Goal 2 - Find components of the net force vector
The previous exact output allows your students see the pattern at work, but an approximate answer is just as easy to obtain by including a decimal point!
Your students can actively decide which results will be important for later use. Define a variable!
Strategic Goal 3 - Use the net force and known force to find the missing force
Strategic Goal 3 - Use the net force and known force to find the missing force
Your students already saw how conversion from polar form works through the exact answer three lines ago! They can actively think about how to use this shortcut to jump ahead.
The input above is another great opportunity to talk with your students about exact vs. approximate results!
Strategic Goal 4 - Put the vector just found back into polar form
Strategic Goal 4 - Put the vector just found back into polar form
Easily done using natural language inputs in Wolfram|Alpha Notebook Edition. We can even refer to the variable defined previously.
A great place to emphasize your student’s knowledge of unit conversions! Radians are standard, but degrees are common in introductory texts.
Physics Is Accessible!
Physics Is Accessible!
The situation can be parsed into a list of strategic goals.
Each goal can be accomplished in a couple of lines of natural language input.
Problem Solved!
Each goal can be accomplished in a couple of lines of natural language input.
Problem Solved!
Use Real Data to Teach Analytical Skills
Use Real Data to Teach Analytical Skills
Use real data to start of an inquiry-driven instructional sequence about plate tectonics
Use real data to start of an inquiry-driven instructional sequence about plate tectonics
Notice how the output might not be what your student first expected, but it makes perfect sense if they read the intuitive Wolfram Language code that ran. This helps teach the skill of refining research questions to be specific to your research!
Refine the driving question to specify the dates you want
Refine the driving question to specify the dates you want
This output is also more complicated than your students may have expected, but that’s because its a REAL data set. A quick alteration of the interpreted result gives only the positions! Your students can either be given this hint by you as the instructor, or you can teach them to look at documentation pages that also clearly explain how to get just the positions.
A quick one-liner based on the interpreted result above
A quick one-liner based on the interpreted result above
Just include “Position” in the third argument for the property that you care about in that large data set. You can provide this as an instructor, or you can help your students learn how to read documentation to figure this out on their own. You can adjust depending on your specific learning goals for the lesson.
Visualize the Data to frame the next question
Visualize the Data to frame the next question
The plot below is made by using only 3 built-in symbols (if you count @), and the variable you helped your students define. You can use Wolfram|Alpha Notebook Edition to blend natural language and Wolfram Language inputs in the way that best serves your learning goals.
Further broaden the original inquiry to see if the patterns your students spot can generalize.
Further broaden the original inquiry to see if the patterns your students spot can generalize.
Now that your students have seen the Wolfram Language one-liner provided by the interpreter, they can use it as a starting place. Changing a specific location Entity to All will get data for all available locations.
Remember that your students can always define a new variable if they think it will be useful for future inputs.
Visualize this new data to continue the cycle of inquiry
Visualize this new data to continue the cycle of inquiry
Now your students have a clear puzzle to solve. Why are all the big earthquakes there?!