You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Special functions
Special functions
as they arise in Mathematica
The error function
The error function
The normal distribution is a function of tremendous importance in probability and statistics. Geometrically, it represents the so-called bell-shaped curve.
In[]:=
normal[x_]=Exp[-/2]
2
x
2π
;bellCurve=Plot[normal[x],{x,-4,4},AspectRatio1/3,ImageSize600,PlotStyleBlack]Out[]=
An important property of this thing is that the total area under the curve is one. Of course, we can check this via integration:
In[]:=
Integrate[normal[x],{x,-Infinity,Infinity}]
Out[]=
1
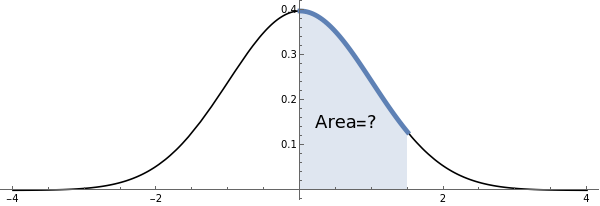
Normal probabilities, say can be expressed as an area under the graph of the normal distribution and over an interval on the real axis. Thus, we need to be able to compute areas like so:
P(0<Z<1.5)
Out[]=
Again, we should be able to do this via integration but we get a weird response when we try Mathematica’s Integrate command:
In[]:=
Integrate[normal[x],x]
Out[]=
1
2
x
2
According to the Documentation, this Erf thing is exactly the value of the following integral:
In[]:=
2Integrate[Exp[-],{t,0,x}]
2
t
π
Out[]=
Erf[x]
In fact, that’s the whole point! We can always use numerical integration to get estimates to normal probabilities:
In[]:=
NIntegrate[normal[x],{x,0,3/2}]
Out[]=
0.433193
Bessel functions
Bessel functions
Here’s an ODE that we’ll meet soon enough:
In[]:=
DSolve[u''[r]+u'[r]/r-λu[r],u[r],r]
Out[]=
u[r]BesselJ0,r+BesselY0,r
λ
1
λ
2
The solution is expressed in terms of special functions called Bessel functions.
In[]:=
DSolve[y''[x]+xy'[x]+(-)y[x]0,y[x],x]
2
x
2
x
2
a
Out[]=
{{y[x]BesselJ[a,x]+BesselY[a,x]}}
1
2
In[]:=
Manipulate[Plot[BesselJ[a,x],{x,-2,T},PlotRangeAll,ImageSize600],{{a,0},Range[0,3]},{{T,12},1,42}]
Out[]=