Pancake-Cutting Problem

cuts

2

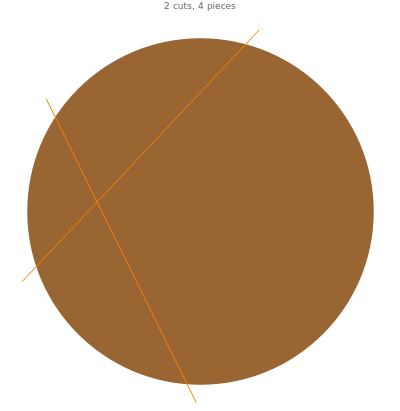
The pancake-cutting problem is to determine the maximum number of pieces

f(n)

into which a pancake can be divided by

n

straight cuts with a knife. The existing

n

cuts divide a new cut into

n+1

segments, each of which divides an existing piece into two pieces. Therefore,

f(n+1)=f(n)+(n+1)

, with initial condition

f(0)=1

. Using Mathematica’s RSolve function, we see that the number of pancake pieces after

n

cuts is

1

2

(

2

n

+n+2)

.

M. Gardner, Martin Gardner’s New Mathematical Diversions from Scientific American, New York: Simon and Schuster, 1966, pp. 235–239.

F. S. Roberts, Applied Combinatorics, New Jersey: Prentice-Hall, 1984, pp. 198–200.

Robert Dickau