Wheel of Congruence Classes of Integers Modulo n

equivalence classes

10

number of circles

3

With respect to a relation

~

, an equivalence class has three properties. Take as an example the integers modulo 3 with respect to congruence.

1. Reflexivity:

a~a

. For example, modulo 3,

1≡1

.

2. Symmetry:

a~b

implies

b~a

. For example, modulo 3,

1≡4

and

4≡1

.

3. Transitivity:

a~b

and

b~c

implies

a~c

. For example, modulo 3,

1≡4

,

4≡7

and

1≡7

.

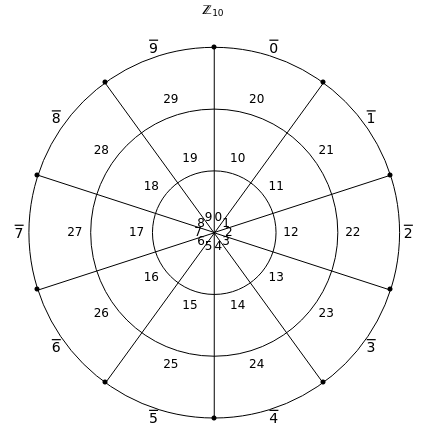
The equivalence classes of the integers modulo

n

can be represented as segments of a wheel, with the congruence class of each of the integers shown. Given a positive integer

n

, each integer

z

satisfies the formula

z=k+nr

, where

0<=k<n

. Here

k

is the value of the equivalence class (shown over-lined),

n

is the order of the additive group



n

and

r

is the segment, starting from 0 in the innermost circle.

External Links

Modular Arithmetic (Wolfram MathWorld)

Congruence (Wolfram MathWorld)

Cyclic Group (Wolfram MathWorld)

Permanent Citation

Theo Williams

"Wheel of Congruence Classes of Integers Modulo n"
http://demonstrations.wolfram.com/WheelOfCongruenceClassesOfIntegersModuloN/
Wolfram Demonstrations Project
Published: September 6, 2023