Orthogonality of Sines and Cosines
Orthogonality of Sines and Cosines
This example comes from[1], Section 9.2, Modeling with First Order Equations.
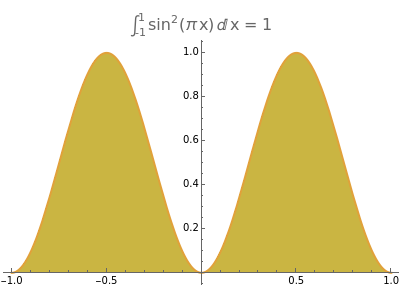
This Demonstration shows the orthogonality of sines and cosines.
For any and ,
m
n
L
∫
-L
mπx
L
nπx
L
For ,
m≠n
L
∫
-L
mπx
L
nπx
L
L
∫
-L
mπx
L
nπx
L
For ,
m=n
L
∫
-L
2
sin
mπx
L
L
∫
-L
2
cos
mπx
L
As you change and , you can see graphically that the areas above and below the axis cancel out in the first three cases. The orthogonal properties of sine and cosine are used in the solution of some classes of partial differential equations in terms of Fourier series.
m
n
References
References
[1] J. R. Brannan and W. E. Boyce, Differential Equations with Boundary Value Problems: An Introduction to Modern Methods and Applications, New York: John Wiley and Sons, 2010.
External Links
External Links
Permanent Citation
Permanent Citation
Stephen Wilkerson
"Orthogonality of Sines and Cosines"
http://demonstrations.wolfram.com/OrthogonalityOfSinesAndCosines/
Wolfram Demonstrations Project
Published: December 7, 2010