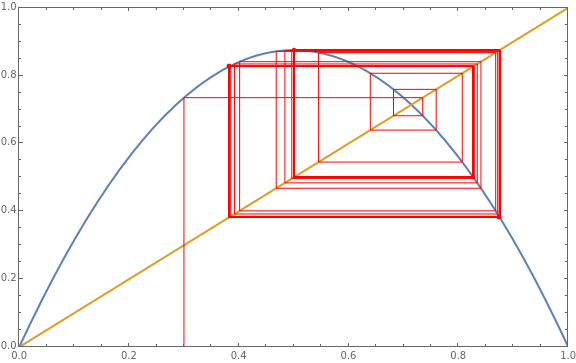
Cobweb Diagram of the Logistic Map

r

3.5

x

0

0.3

number of iterations

500

number of dropped iterations

0

The logistic map, a popular example of a period-doubling cascade developing to chaos, obeys the recurrence

x

n

=r

x

n-1

(1-

x

n-1

)

. The red cobweb diagram traces out the orbit of

x

for a given value of the parameter

r

. The orbit is chaotic when the cobweb diagram becomes dense.

Use the "

r

" slider to see periodic or chaotic orbits or one with a fixed point as the limit.

Use the "

x

0

" slider to change the starting value. For a suitably high number of dropped iteration, the starting value should have a negligible affect on the plot, except in the chaotic regime.

Use the "number of iterations" slider to set the maximum

n

chosen for plotting

x

n

.

Use the "number of dropped iterations" slider to set the number of the initial iterations that are not included in the plot. If

n=0

, no iterations are dropped.

Details

Snapshot 1: period 2 orbit

Snapshot 2: period 4 orbit

Snapshot 3: chaotic orbit

External Links

Web Diagram (Wolfram MathWorld)

Logistic Map (Wolfram MathWorld)

Cobweb Diagrams of Elementary Cellular Automata

Cobweb Diagram for Generalized Logistic Maps with z-Unimodality

Three Views of the Logistic Map

Permanent Citation

Kevin Reiss

"Cobweb Diagram of the Logistic Map"
http://demonstrations.wolfram.com/CobwebDiagramOfTheLogisticMap/
Wolfram Demonstrations Project
Published: May 20, 2021