We are glad you are taking a moment to explore the Wolfram Language’s hypergraph capabilities. In this notebook, we’ll start by showing how you can represent and plot hypergraphs, then walk you through two simple algorithms for computing transversal hypergraphs. Get an overview of all the functionalities available in the Wolfram Language in the Wolfram Language & System Documentation Center.
Recall that a hypergraph consists of the set of vertices and the set of hyperedges, each of which is a non-empty subset of those vertices. When it is understood that every vertex lies in at least one hyperedge, then we can let also refer to its set of hyperedges.
H=(V,E)
V
E
H
Clickinthecode,thenholdandpresstorunit.
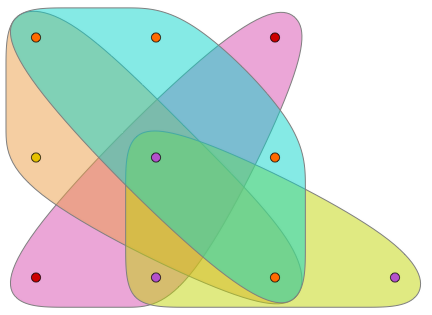
Represent a hyperedge as a list of vertices, and a hypergraph as a list of edges and isolated vertices:
In[1]:=
hypergraph={{a,b,c,d},{b,c},{c,d,e},f,g};
Plot hypergraphs using the built-in function CommunityGraphPlot, which creates a colored region for each hyperedge:
hypergraphPlot[hyp_]:=CommunityGraphPlot[Graph[DeleteDuplicates[Flatten[hyp,1]],{},VertexLabels"Name"],Select[hyp,ListQ],CommunityRegionStyleRandomColor[RGBColor[_,_,_,.5],5]]hypergraphPlot[hypergraph]
Out[3]=
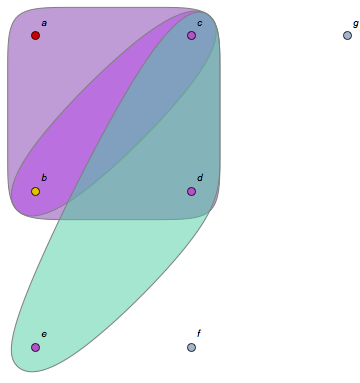
A transversal of a hypergraph is a subset of that has a non-empty intersection with each hyperedge in . A minimal transversal is a transversal containing no other transversal as a proper subset. The transversal hypergraph of H is the hypergraph , where is the subset of consisting of all vertices appearing in an edge of , and is the collection of all minimal transversals of . For instance, the hypergraph below is the transversal hypergraph of the hypergraph above:
T
H=(V,E)
U
V
E
Tr(H)
(U,F)
U
V
H
F
H
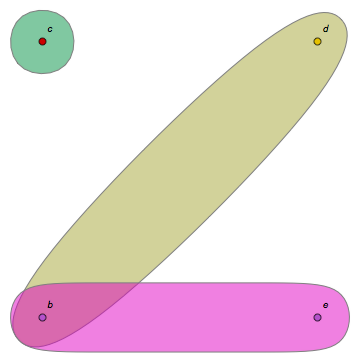
hypergraphPlot[{{c},{b,d},{b,e}}]
Out[4]=
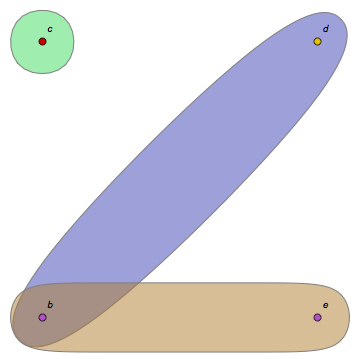
Let be the set of minimal hyperedges of (i.e. is obtained from by deleting all isolated vertices as well as any hyperedge that properly contains another hyperedge). Note that :
min(H)
H
min(H)
H
Tr(H)=Tr(min(H))
min[hyp_]:=DeleteDuplicates[SortBy[Select[hyp,ListQ],Length],Function[{small,large},SubsetQ[large,small]]]min[hypergraph]hypergraphPlot[%]
Out[6]=
{{b,c},{c,d,e}}
Out[7]=
Let be a hypergraph, and be the hypergraph obtained from by adding an extra hyperedge . Note that if is a minimal transversal of and , then either is a minimal transversal of or contains the minimal transversal of as a subset. Conversely, any minimal transversal of is either a minimal transversal of that shares a vertex with , or a minimal transversal of that didn’t already intersect plus any single vertex of . Hence we have the identity , which we encode in the function below that takes as input and :
H
H'
H
e
h
H
v∈e
h⋃{v}
H'
h
H'
H'
H
e
H
e
e
Tr(H')=min({h⋃{v}:h∈Tr(H)∧v∈e})
Tr(H)
e
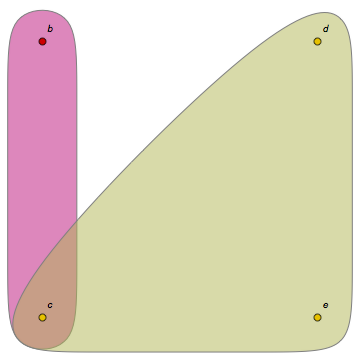
extend[trHyp_,edge_]:=min[Map[Composition[DeleteDuplicates,Apply[Append]],Tuples[{trHyp,edge}]]]extend[{{b},{c}},{c,d,e}]
Out[9]=
{{c},{b,d},{b,e}}
Berge’s algorithm for computing the transversal hypergraph of simply starts with the empty hypergraph and performs this extension edge by edge of to eventually obtain :
H
min(H)
Tr(H)
transHypBerge[hypergraph_]:=Fold[extend,{{}},min[hypergraph]]transHypBerge[hypergraph]hypergraphPlot[%]
Out[11]=
{{c},{b,d},{b,e}}
Out[12]=
Unfortunately, Berge’s algorithm isn’t particularly efficient, and doesn’t run very fast on hypergraphs with many vertices:
Berge’s algorithm can be greatly optimized, however, by treating vertices that appear in precisely the same hyperedges of the relevant hypergraph as a single “block” vertex when appropriate. This is the approach of Kavvadias and Stavropoulos.
This partial hypergraph would have the following blocks...
... giving it the following blocked form:
This blocked partial hypergraph would have the following transversal hypergraph...
... and designate the remaining blocks as “split blocks”...
Update the list of blocks:
Perform the same extension used previously in Berge’s algorithm:
Running this algorithm of Kavvadias and Stavropoulos on the hypergraph for which Berge’s algorithm took a bit of time...
... we see that the timing is greatly improved...
... and that we do, in fact, get the same transversal hypergraph (even if the representations might be different):
... and compare the two algorithms’ running times and outputs: