In[]:=
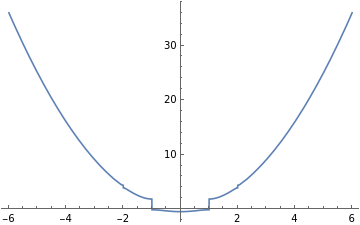
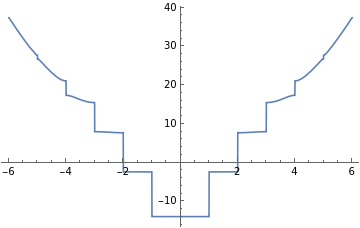
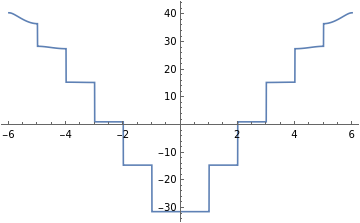
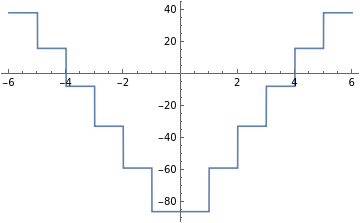
Plot[MathieuCharacteristicA[r,1],{r,-6,6}]Plot[MathieuCharacteristicA[r,10],{r,-6,6}]Plot[MathieuCharacteristicA[r,20],{r,-6,6}]Plot[MathieuCharacteristicA[r,50],{r,-6,6}]
Out[]=
Out[]=
Out[]=
Out[]=
In[]:=
The index function k(ng, n) in the book doesn't work outside [-0.5, 0.5].
The formula in Koch et al. (2007) works in all ranges but generates the wrong order 0 -> 2 -> 1 -> 4 -> 3 -> 6 -> 5 ->...
So I implemented the modified version of Koch's one.
The formula in Koch et al. (2007) works in all ranges but generates the wrong order 0 -> 2 -> 1 -> 4 -> 3 -> 6 -> 5 ->...
So I implemented the modified version of Koch's one.
In[]:=
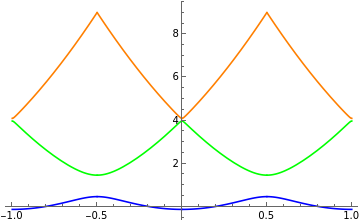
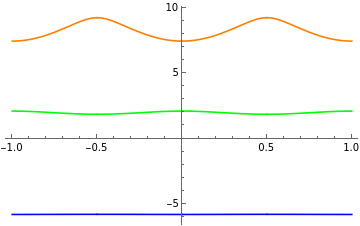
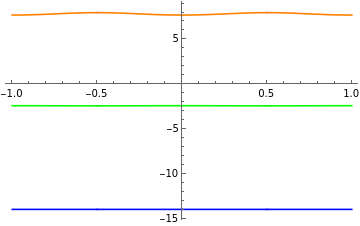
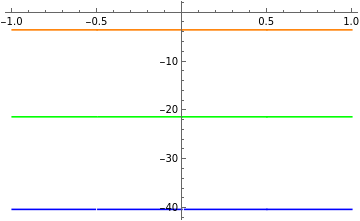
k[ng_,n_]:=(m=n-((-1)^n)*Sign[n];Sum[Mod[Round[2*ng+l/2],2]*(Round[ng]+l*(-1)^m*Quotient[(m+1),2]), {l,{-1,1}}])r[ng_,n_]:=-2*ng+2*k[ng,n]e[ng_,n_,ejec_]:=MathieuCharacteristicA[r[ng,n],ejec/2](*ejec=EJ/EC*)Plot[{e[ng,0,1],e[ng,1,1],e[ng,2,1]},{ng,-1,1},PlotStyle{Blue,Green,Orange}]Plot[{e[ng,0,10],e[ng,1,10],e[ng,2,10]},{ng,-1,1},PlotStyle{Blue,Green,Orange}]Plot[{e[ng,0,20],e[ng,1,20],e[ng,2,20]},{ng,-1,1},PlotStyle{Blue,Green,Orange}]Plot[{e[ng,0,50],e[ng,1,50],e[ng,2,50]},{ng,-1,1},PlotStyle{Blue,Green,Orange}]
Out[]=
Out[]=
Out[]=
Out[]=
In[]:=
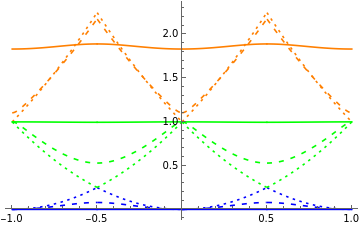
gap[q_]:=MathieuCharacteristicA[r[10^-10,1],q]-MathieuCharacteristicA[r[10^-10,0],q](*Avoidsingularityatng=0*)e[ng_,n_,ejec_]:=(MathieuCharacteristicA[r[ng,n],ejec/2]-MathieuCharacteristicA[r[10^-10,0],ejec/2])/gap[ejec/2](*Avoidsingularityatng=0*)Show[Plot[{e[ng,0,0.02],e[ng,1,0.02],e[ng,2,0.02]},{ng,-1,1},PlotStyle{{Dashing[Small],Blue},{Dashing[Small],Green},{Dashing[Small],Orange}}],Plot[{e[ng,0,2],e[ng,1,2],e[ng,2,2]},{ng,-1,1},PlotStyle{{Dashing[Medium],Blue},{Dashing[Medium],Green},{Dashing[Medium],Orange}}],Plot[{e[ng,0,16],e[ng,1,16],e[ng,2,16]},{ng,-1,1},PlotStyle{{Blue},{Green},{Orange}}]]
Out[]=
In[]:=
psi0[z_,ejec_,n_,ng_]:=MathieuC[MathieuCharacteristicA[r[ng+10^-10,n],ejec/2],ejec/2,(z+Pi)/2](*Avoidsingularityat2ngisinteger*)psi1[z_,ejec_,n_,ng_]:=MathieuS[MathieuCharacteristicB[r[ng+10^-10,n],ejec/2],ejec/2,(z+Pi)/2](*Avoidsingularityat2ngisinteger*)psi[z_,ejec_,n_,ng_]:=(Exp[I*ng*z]/Sqrt[2*Pi])*(psi0[z,ejec,n,ng]+I*psi1[z,ejec,n,ng])Show[Plot[Abs[psi[z,2,0,0]]^2,{z,-Pi,Pi},PlotStyle{Blue},PlotRangeAll],Plot[Abs[psi[z,2,1,0]]^2,{z,-Pi,Pi},PlotStyle{Green},PlotRangeAll],Plot[Abs[psi[z,2,2,0]]^2,{z,-Pi,Pi},PlotStyle{Orange},PlotRangeAll]]Show[Plot[Abs[psi[z,2,0,1/2]]^2,{z,-Pi,Pi},PlotStyle{Blue},PlotRangeAll],Plot[Abs[psi[z,2,1,1/2]]^2,{z,-Pi,Pi},PlotStyle{Green},PlotRangeAll],Plot[Abs[psi[z,2,2,1/2]]^2,{z,-Pi,Pi},PlotStyle{Orange},PlotRangeAll]]