Algebraic Solution of the Plemelj Triangle Construction Problem
Algebraic Solution of the Plemelj Triangle Construction Problem
This problem asks for the construction of a triangle with ruler and compass given the length of the base (for simplicity, let ), the length of the altitude from to and the difference of the angles and . The problem was posed to Plemelj by his math teacher, Borstner, when Plemelj was about 16 years old.
ABC
AB=c
c=1
h
c
C
AB
α-β
α=∠BAC
β=∠ABC
Plemelj solved the problem using trigonometry, and later found a geometric construction. The starting point was the identity (cotα+cotβ)=c, from which he derived the equation . This equation can be transformed by substituting . Eliminating the square root gives a quadratic equation for , which means that it and can be constructed by using a straight edge and a compass.
h
c
2sinγ-ccosγ=ccos(α-β)
h
c
cos(γ)=
1-γ
2
sin
sinγ
γ
Using the formula , where is the radius of the circumscribed circle, gives a quadratic equation for .
sinγ=c/2R
R
R
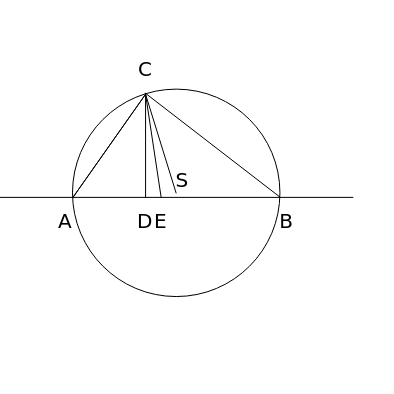
To construct the triangle, first draw a vertical straight line of length and a horizontal line through . Then draw line so that . If is the altitude on , then is the bisector of angle . Draw the straight line so that . Then measure out a distance from on the horizontal line to find .
CD
h
c
D
CE
∠ECD=1/2(α-β)
CD
c
CE
γ
CB
∠DCE=1/2γ
c
B
A
To use in the construction, we must know that the angle between the altitude and the line from to the center of the circumscribed circle of the triangle is .
R
∠DCS
CS
C
α-β
So on the line through that has the angle with , measure out a distance to find the point . Then draw a circumscribed circle . Points and are intersections of by the horizontal line through .
C
α-β
CD
R
S
σ
A
B
σ
D
The solutions can be checked to verify that they give the same result.
Details
Details
Plemelj's most original contribution is the elementary solution he provided for the Riemann–Hilbert problem about the existence of a differential equation with given monodromy group[1, 2]. Plemelj's first solution of the triangle construction problem was given in[2]. We take his trigonometry explanation from[3, pp. 191]. He also noted that he had made nine original solutions of the problem, and that he had also known about two textbook solutions.
The text in[3] is from a talk Plemelj gave in 1949 at the First Congress of Yugoslav Societies of Mathematicians, Physicists and Astronomers in Bled (Slovenia). The talk was published in 1951 in Belgrade in the proceedings of the congress.
Two different solutions of the problem are published in[4], and one in[5].
References
References
[2] J. J. O'Connor and E. F. Robertson. "Josip Plemelj." MacTutor. www-history.mcs.st-andrews.ac.uk/Biographies/Plemelj.html.
[3] J. Plemelj, Iz mojega življenja in dela (From My Life and Work), Obzornik mat. fiz., 39, 1992 pp. 188–192.
[4] D. S. Modic, Triangles, Constructions, Algebraic Solutions (in Slovenian), Ljubljana: Math Publishers, 2009.
[5] I. Pucelj, "Plemelj's Triangle and Fixed Points of Transformations" (in Slovenian), Obzornik mat. fiz., 62(1), 2015 pp. 12–14.
External Links
External Links
Permanent Citation
Permanent Citation
Izidor Hafner
"Algebraic Solution of the Plemelj Triangle Construction Problem"
http://demonstrations.wolfram.com/AlgebraicSolutionOfThePlemeljTriangleConstructionProblem/
Wolfram Demonstrations Project
Published: June 1, 2017