Cubic Equation of State for the Compressibility Factor
Cubic Equation of State for the Compressibility Factor
In the Soave–Redlich–Kwong (SRK) equation of state (EOS), the compressibility factor occurs as a solution of the following cubic equation:
f(Z)=-+(A-B-)Z-AB=0
3
Z
2
Z
2
B
where and with , , , and . Here is the acentric factor, and are the critical temperature and pressure, and = is the reduced pressure.
A=
aP
2
(RT)
B=
bP
RT
a=0.42748α
2
(R)
T
c
P
c
b=0.08664R/
T
c
P
c
α=
2
1+m1-
T
re
m=0.480+1.574ω-0.176
2
ω
ω
T
c
P
c
T
re
T
T
c
When and = are greater than one, the supercritical behavior is observed with varying continuously between low (close to zero, liquid-like behavior) and high values (near one, vapor-like behavior).
T
r
P
r
P
P
c
Z
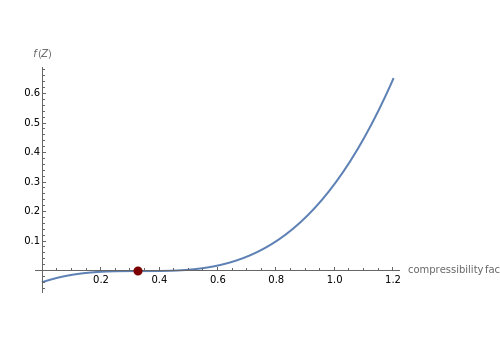
For specific values of and (when , the saturation pressure, and ), one gets three roots with the smallest and largest corresponding to the liquid and vapor phases. The intermediate value of has no physical significance.
T
r
P
r
P=
sat
P
T<
T
c
Z
The Demonstration plots for ethane (=305.43K, =48.84bar, and ) and displays the location and values of its real roots.
f(Z)
T
c
P
c
ω=0.09860