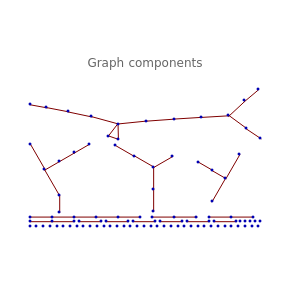
Giant Component in Random Graph
Giant Component in Random Graph
A random graph is a graph with nodes where the probability of finding an edge between two nodes is . When tends to a constant (as grows), the graph will almost surely contain a "giant" connected component, absorbing a considerably large fraction of the nodes. This phenomenon is often mentioned as an example of emergence in random graph behavior.
G(n,p)
n
p
n×p
c>1
n
Details
Details
The emergence of a giant connected component plays a crucial role in the theory of autocatalytic chemical networks, which attempts to explain the appearance of life in the universe ("abiogenesis") as a self-organization phenomenon occurring within chemical systems. The idea was first proposed by Stuart Kauffman in 1995.
See the actual graph growth process at Giant Component.
S. Kauffman, At Home in the Universe: The Search for the Laws of Self-Organization and Complexity, Oxford: Oxford Univ. Press, 1995.
External Links
External Links
Permanent Citation
Permanent Citation
Tommaso Bolognesi
"Giant Component in Random Graph"
http://demonstrations.wolfram.com/GiantComponentInRandomGraph/
Wolfram Demonstrations Project
Published: March 7, 2011