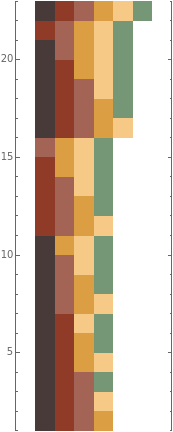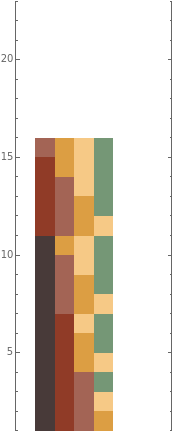Banzhaf Power Index
Banzhaf Power Index
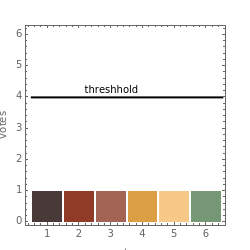
The Banzhaf index is a measure of how probable it is that someone's vote will change the outcome of an election in settings in which voters may have unequal numbers of votes. This Demonstration examines a scenario with six voters, each of whom have a user-selectable number of votes. You can also determine the percentage of total votes needed to win. From this data, the Demonstration shows all the winning coalitions that can form and all the members of each coalition ("the swing voters") who, if they had voted differently, would have changed the outcome of the election. The Banzhaf index, which ranges from 0 to 1, is the percentage of times each voter is a swing voter over all possible winning coalitions.
Details
Details
The Banzhaf index is closely related to the Shapley value, often used in cooperative games.
Snapshot 1: the percentage of votes needed to win affects the power index
Snapshot 2: sometimes, parties with different amounts of raw voting power have the same power index
Snapshot 3: only two parties have any real power
Snapshot 4: a four party system in which the second party has somewhat more votes but has no more power when a two thirds majority is needed
Snapshot 5: a four party system in which the second party has somewhat more votes but has considerably more power
External Links
External Links
Permanent Citation
Permanent Citation
Seth J. Chandler
"Banzhaf Power Index"
http://demonstrations.wolfram.com/BanzhafPowerIndex/
Wolfram Demonstrations Project
Published: September 28, 2007