Using Zeta Zeros to Compute the Chebyshev Psi Function

start x axis at (from 0 to 1000)

length of x axis (from 10 to 100)

pairs of ζ zeros (from 0 to 200)

always show estimate of ψ using no ζ zeros

display ψ values in a tooltip

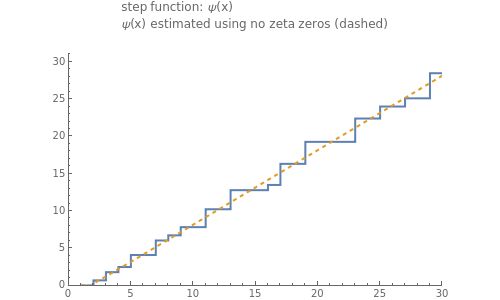
Chebyshev's psi (

) function is important in number theory. It is defined as the logarithm of the least common multiple of the integers from 1 through

. The graph of

ψ(x)

is an irregular step function.

This Demonstration illustrates the remarkable fact that we can approximate the jumps of this step function by using a sum that involves zeros of the Riemann zeta function

ζ(s)

Details

Snapshot 1: the graphs of the step function

ψ(x)

and the formula using no zeta zeros

Snapshot 2: the graphs of

ψ(x)

and the formula using 30 pairs of zeta zeros

Snapshot 3: in order to hit the small jump in

x=128

, at least 70 zeta zeros are needed

ψ(x)

can be defined as

∑

p≤x



log

(x)log(p)

, where the sum is over the primes

p≤x

, and

⌊.⌋

denotes the floor function. For example,

ψ(10)=⌊

log

(10)⌋log(2)+⌊

log

(10)⌋log(3)+⌊

log

(10)⌋log(5)+⌊

log

(10)⌋log(7)

≃

⌊3.3⌋log(2)+⌊2.1⌋log(3)+⌊1.4⌋log(5)+⌊1.2⌋log(7)

3log(2)+2log(3)+log(5)+log(7)

log(

×5×7)=log(2520)

Note that 2520 is the least common multiple of the integers 1 through 10.

ψ(x)

behaves as follows: when

reaches a prime power

, then

ψ(x)

increases by

log(p)

. After that,

ψ(x)

remains constant until

reaches the next prime power. This means the graph of

ψ(x)

is a step function that jumps up at powers of primes.

This Demonstration uses von Mangoldt's formula to calculate

ψ(x)

ψ(x)≃x-

′

(0)

ζ(0)

-2Re

∑

k=1

∞

∑

k=1

-2k

where

is the

complex zero of the Riemann zeta function. See[1] for general information about the

function. See p. 104 of[2] for a proof of this formula.

′

(0)/ζ(0)

is a constant that simplifies to

log(2π)

, which is about 1.837877;

is the dominant term in the formula. It can be proven that as

approaches

∞

, the ratio

ψ(x)/x

approaches 1. This fact is equivalent to the prime number theorem, which states that as

approaches

∞

, the ratio

π(x)

log(x)

approaches 1, where

π(x)

is the number of primes less than or equal to

The first three complex zeros of the zeta function are approximately

1/2+14.135i

1/2+21.022i

, and

1/2+25.011i

. The zeros occur in conjugate pairs, so if

a+bi

is a zero, then so is

a-bi

. The important Riemann hypothesis is the unproven conjecture that all these complex zeros have real part 1/2. So far, it has been verified that the first

complex zeros do, indeed, have real part 1/2 (see[3]).

If you use the slider to choose, say, one pair of zeta zeros, then the first sum in the above formula, in effect, combines two terms corresponding to the first conjugate pair of zeta zeros

1/2+14.135i

and

1/2-14.135i

. So, when these terms are added, their imaginary parts cancel while their real parts add. The

2Re(…)

applied to the first sum is simply an efficient way to combine the two terms for each pair of zeta zeros.

Notice that the second sum has the same form as the first, except that the second sum extends over the so-called "trivial" zeros of the zeta function, namely,

-2k=-2,-4,-6,…

. The second sum is small when

is large.

All known zeta zeros have multiplicity 1, which is assumed in the formula. At those values of

where

ψ(x)

jumps from

y=a

y=b

, the formula converges to the midpoint,

y=(a+b)/2

, as