Temperature Dependance of Photo-Induced Electron Transfer 1: CME and MLJ; (Constant Epsilon and Gibbs Free Energy)
Temperature Dependance of Photo-Induced Electron Transfer 1: CME and MLJ; (Constant Epsilon and Gibbs Free Energy)
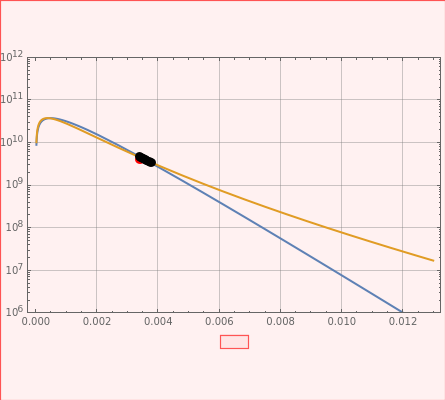
This Demonstration shows the effect of temperature on the rate of electron transfer. No change of the dielectric constant with temperature is taken into account, so far.
It compares the classical Marcus equation (CME, blue) to the semiclassical (MLJ) approach (yellow) using log plots. The three-dimensional plots in earlier Demonstrations (see Related Links) are linear plots in the rate . At very low temperatures, both models become inaccurate (see below).
k
Details
Details
This Demonstration describes the semiclassical Marcus model (also called Marcus–Levich–Jortner theory, MLJ) and compares it to the classical Marcus equation (CME). The plots show log as a function of inverse temperature, in an Arrhenius-type analysis. Experimental data is given in black, as an example. For MLJ, use and for fitting this experimental data. For CME, it is the start data. Freezing of the solvent is not taken into account within the model. Experiments normally take into account the solidification (freezing), as well as the boiling point of a solvent (if a solvent is used). The high temperature range, above 1000 K (close to ), is just presented for convenience (T will become a rather high energy).
k
ΔG=-0.475eV
V=40
-1
cm
x=0
k
B
Nobel Prize winner Rudolph Marcus developed the theory of electron transfer[1]. The CME is based on two simultaneous quadratic relations involving the driving force , the internal and external (solvent) reorganization energies and and the electronic coupling . The CME underestimates the electron transfer rate in the inverted region[2, 3]. Therefore, we need the MLJ equation:
-ΔG
λ
I
λ
S
V
k
ET
π
2
ℏ
λ
S
k
B
2
V
∞
∑
m=0
-S
e
m
S
m!
2
(ΔG++mℏω)
λ
S
4T
λ
S
k
B
where . This plot of log versus "1/temperature" is shown in yellow.
S=/ℏω
λ
I
k
The CME, shown in blue, is represented by:
k
ET
π
2
ℏ
λ
T
k
B
2
V
2
(ΔG+)
λ
T
4T
λ
T
k
B
You can change the axes with the control sliders. You can also change the number of plot points. More plot points give greater detail, but at the cost of slowing the computation. The temperature of the red dot is indicated, as well as the activation energies () for both models. For clarity, the total reorganization energy and the Huang–Rhys factors are also indicated.
E
a
The Closs and Miller data[4], provided the first experimental proof of the inverted region.
We apply the semiclassical Marcus expression to the inverted region. If is much larger than the total , then inverted region effects are apparent. The enhanced rate (relative to CME) in the inverted region is related to the overlap of vibrational wavefunctions, which contribute to the Franck–Condon weighted density of states. The Huang–Rhys factor is related to the vibronic coupling, which is electron-phonon coupling (represented by the symbol in the MLJ equation). This effect is also important at low temperature.
-ΔG
λ=+
λ
I
λ
S
S=/ℏω
λ
i
We can approximate the measured rates[5] with these equations by adjusting the input data.
The parameter in the summation factor determines how many transfer channels contribute to the total rate[3]. Often only six channels are needed. Additional information on Marcus theory and electron transfer is given in[6–11]. If , the equation behaves like the CME.
m
m=0
The MLJ theory is especially evident in the inverted region. As the value of approaches twice the total , inverted region effects start playing a more important role. MLJ becomes a better approximation at lower temperatures. But for very low temperatures, there are modified equations (see below). For very low temperatures, both vibrations should be treated quantum mechanically.
-ΔG
λ
As for validity of the model, the (single mode) MLJ theory can be applied: above , with the electronic coupling between and ; in polar liquids, with ; and in molecular solids, with (pertaining to both intermolecular phonons and solid matrix phonons with energies of 0.00124 to 0.0124 eV). Intramolecular frequencies can range between 300 and (0.0372 and 0.372 eV). It is also possible to apply the multi-mode MLJ equation[2].
~77K
~1
~200
-1
cm
ω≈1-10
-1
cm
ω≈10-100
-1
cm
ω
i
~3000
-1
cm
Thus, in the MLJ theory, the internal is treated quantum mechanically. The solvent reorganization is treated classically.
λ
In the intermediate temperature range, the most common one, the solvent (environmental) vibrational modes can be treated classically if , where is an average solvent vibrational frequency. The intramolecular vibrations are quantum, that is, .
ℏ≪T
ω
S
k
B
ω
S
ℏω>T
k
B
In general, a vibration can be treated as classical if , and as quantum if . You should monitor these values as temperature is varied.
ω
ℏω≪T
k
B
ℏω≫T
k
B
More information on effects of low reorganization energies and can be found in the references. Oscillations in the bell-shaped Marcus curve (resonance-type effects in the Franck–Condon factor) are discussed in[12–17]. These papers also contain temperature-dependant data.
ΔG
Below 10 K, more complex models are needed[18, 19].
The test data (black points) comes from[20]. Other temperature-dependant electron transfer data can be found, for instance, in[21–23].
Snapshot 1: zoom into the plot showing the fit of the experimental data with the CME
Snapshot 2: zoom into the plot showing the fit of the experimental data with the more elaborate MLJ model
Snapshot 3: under optimal conditions, both models show that the rate is virtually independent of temperature
References
References
[1] R. A. Marcus, "Electron Transfer Reactions in Chemistry: Theory and Experiment (Nobel Lecture)," Angewandte Chemie International Edition, 32(8), 1993 pp. 1111–1121. doi:10.1002/anie.199311113.
[2] S. Chaudhuri, S. Hedström, D. D. Méndez-Hernández, H. P. Hendrickson, K. A. Jung, J. Ho and V. S. Batista, "Electron Transfer Assisted by Vibronic Coupling from Multiple Modes," Journal of Chemical Theory and Computation, 13(12), 2017 pp. 6000–6009. doi:10.1021/acs.jctc.7b00513.
[3] P. F. Barbara, T. J. Meyer and M. A. Ratner, "Contemporary Issues in Electron Transfer Research," Journal of Physical Chemistry, 100(31), 1996 pp. 13148–13168. doi:10.1021/jp9605663.
[4] G. L. Closs and J. R. Miller, "Intramolecular Long-Distance Electron Transfer in Organic Molecules," Science, 240(4851), 1988 pp. 440–447. doi:10.1126/science.240.4851.440.
[5] P. Hudhomme and R. M. Williams, "Energy and Electron Transfer in Photo- and Electro-active Fullerene Dyads," Handbook of Carbon Nano Materials (F. D'Souza and K. M. Kadish, eds.), Hackensack, NJ: World Scientific, 2011 pp. 545–591. doi:10.1142/9789814327824_0017.
[6] R. M. Williams. "Introduction to Electron Transfer." (Nov 21, 2021) doi:10.13140/RG.2.2.16547.30244.
[7] R. M. Williams. Photoinduced Electron Transfer—The Classical Marcus Theory [Video]. (Jun 24, 2024) youtu.be/YFzeMMOvhl0.
[8] R. M. Williams. Photoinduced Electron Transfer—The Semi-classical Marcus–Levich–Jortner Theory[Video]. (Jun 24, 2024) youtu.be/GnPIbH6nM9o.
[9] R. M. Williams. University of Amsterdam. (Jun 24, 2024) www.uva.nl/en/profile/w/i/r.m.williams/r.m.williams.html.
[10] J. Idé and G. Raos. "ChargeTransport: Charge Transfer Rates and Charge Carrier Mobilities." (Jun 24, 2024) cran.r-project.org/src/contrib/Archive/ChargeTransport.
[12] A. Sarai, "Energy-Gap and Temperature Dependence of Electron and Excitation Transfer in Biological Systems," Chemical Physics Letters, 63(2), 1979 pp. 360–366. doi:10.1016/0009-2614(79)87036-0.
[13] J. R. Miller, J. V. Beitz and R. K. Huddleston, "Effect of Free Energy on Rates of Electron Transfer between Molecules," Journal of the American Chemical Society, 106(18), 1984 pp. 5057–5068. doi:10.1021/ja00330a004.
[14] M. R. Gunner, D. E. Robertson and P. L. Dutton, "Kinetic Studies on the Reaction Center Protein from Rhodopseudomonas sphaeroides: The Temperature and Free Energy Dependence of Electron Transfer between Various Quinones in the QA Site and the Oxidized Bacteriochlorophyll Dimer," Journal of Physical Chemistry, 90(16), 1986 pp. 3783–3795. doi:10.1021/j100407a054.
[15] R. Rujkorakarn and F. Tanaka, "Three-Dimensional Representations of Photo-induced Electron Transfer Rates in Pyrene--N,N'-dimethylaniline Systems Obtained by Three Electron Transfer Theories," Journal of Molecular Graphics and Modelling, 27(5), 2009 pp. 571–577. doi:10.1016/j.jmgm.2008.09.008.
()
CH
2
n
[16] T. Unger, S. Wedler, F.-J. Kahle, U. Scherf, H. Bässler and A. Köhler, "The Impact of Driving Force and Temperature on the Electron Transfer in Donor–Acceptor Blend Systems," The Journal of Physical Chemistry C, 121(41), 2017 pp. 22739–22752. doi:10.1021/acs.jpcc.7b09213.
[17] W. W. Parson, "Generalizing the Marcus Equation," The Journal of Chemical Physics, 152(18), 2020 184106. doi:10.1063/5.0007569.
[18] J. B. Kelber, N. A. Panjwani, D. Wu, R. Gómez-Bombarelli, B. W. Lovett, J. J. L. Morton and H. L. Anderson, "Synthesis and Investigation of Donor–Porphyrin–Acceptor Triads with Long-Lived Photo-Induced Charge-Separate States," Chemical Science, 6(11), 2015 pp. 6468–6481. doi:10.1039/C5SC01830G.
[19] G. Lanzani, "Charge Transfer and Transport," The Photophysics behind Photovoltaics and Photonics, Weinheim: Wiley-VCH, 2012 pp. 145–176. doi:10.1002/9783527645138.ch8.
[20] R. M. Williams, M. Koeberg, J. M. Lawson, Y.-Z. An, Y. Rubin, M. N. Paddon-Row and J. W. Verhoeven, "Photoinduced Electron Transfer to across Extended 3- and 11-Bond Hydrocarbon Bridges: Creation of a Long-Lived Charge-Separated State," The Journal of Organic Chemistry, 61(15), 1996 pp. 5055–5062. doi:10.1021/jo960678q.
C
60
[21] J. Kroon, H. Oevering, J. W. Verhoeven, J. M. Warman, A. M. Oliver, and M. N. Paddon-Row, "Temperature Effects on Intramolecular Electron Transfer Kinetics under "Normal", "Inverted", and "Nearly Optimal" Conditions," The Journal of Physical Chemistry, 97(19), 1993 pp. 5065–5069. doi:10.1021/j100121a036.
[22] Y. Zeng and M. B. Zimmt, "Symmetry Effects on Electron-Transfer Reactions: Temperature Dependence as a Diagnostic Tool," The Journal of Physical Chemistry, 96(21), 1992, pp. 8395–8403. doi:10.1021/j100200a035.
[23] K. K. Mentel, A. Serra, P. E. Abreu and L. G. Arnaut, "Higher Activation Barriers Can Lift Exothermic Rate Restrictions in Electron Transfer and Enable Faster Reactions," Nature Communications, 9(1), 2018 2903. doi:10.1038/s41467-018-05267-5.
External Links
External Links
Permanent Citation
Permanent Citation