Wolfram Cloud Document

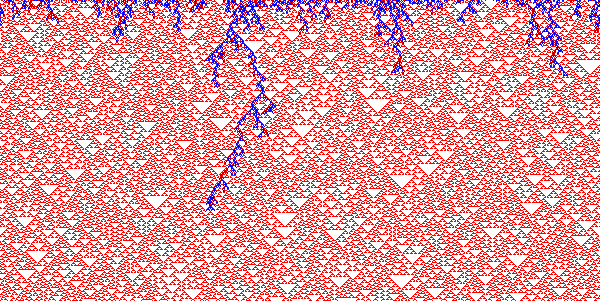
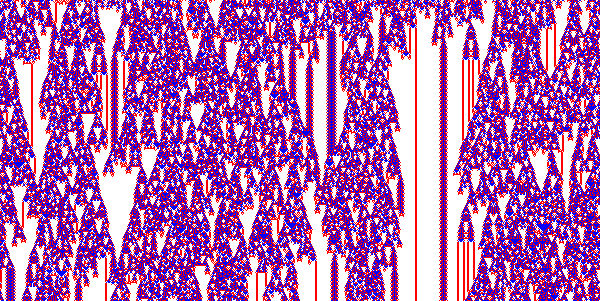
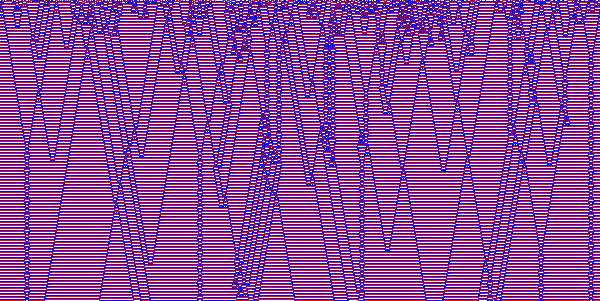
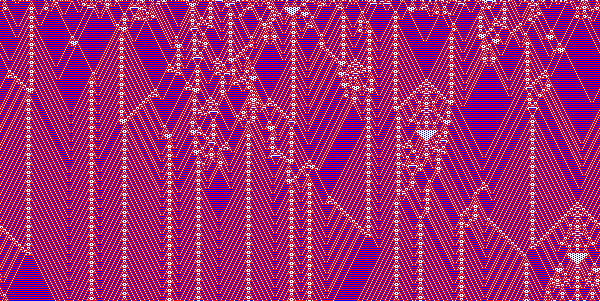
Totalistic k=3

In[]:=

ResourceFunction["InteractiveListSelector"][Table[ArrayPlot[CellularAutomaton[{n,{3,1},1},SeedRandom[24142];RandomInteger[2,200],150],Frame->False,ColorRules->{0->White,1->Blue,2->Red},PixelConstrained1]->n,{n,0,3^7-1,3}]]

Out[]=

{42,42,51,114,195,231,288,306,318,357,384,426,438,555,600,627,705,843,792,963,966,924,1041,1038,1086,1572,1599,1521,1659,1815,2007,2049}

In[]:=

ResourceFunction["InteractiveListSelector"][Table[ArrayPlot[CellularAutomaton[{n,{3,1},1},SeedRandom[24142];RandomInteger[2,200],150],Frame->False,ColorRules->{0->White,1->Blue,2->Red},PixelConstrained1]->n,{n,1,3^7-1,3}]]

Out[]=

{148,178,397,964,856,1258,2050}

{42,42,51,114,195,231,288,306,318,357,384,426,438,555,600,627,705,843,792,963,966,924,1041,1038,1086,1572,1599,1521,1659,1815,2007,2049}

In[]:=

ResourceFunction["InteractiveListSelector"][Labeled[ArrayPlot[CellularAutomaton[{#,{3,1},1},SeedRandom[24143];RandomInteger[2,600],300],Frame->False,ColorRules->{0->White,1->Blue,2->Red},PixelConstrained1],#]->#&/@{42,42,51,114,195,231,288,306,318,357,384,426,438,555,600,627,705,843,792,963,966,924,1041,1038,1086,1572,1599,1521,1659,1815,2007,2049,148,178,397,964,856,1258,2050}]

Out[]=

