In[]:=
A[n_,k_]:=(p/q)^k((1-p)/(1-q))^(n-k);a[n_]:=(p-q)^2*Sum[Binomial[n,k]p^k(1-p)^(n-k)A[n,k]/((1+A[n,k])(1-q+(1-p)A[n,k])(q+pA[n,k])),{k,0,n}];q=1/5;p=4/5;DiscretePlot[a[n],{n,1,100},PlotRange{{1,40},{0,0.1}}]
Out[]=
In[]:=
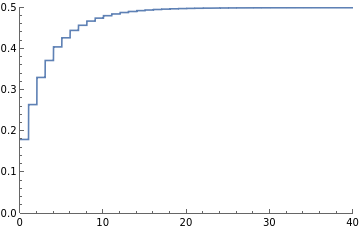
sumA[m_]:=Sum[a[n],{n,0,m}];Plot[sumA[n],{n,0,40},PlotRange{{0,40},{0,1/2}}]
Out[]=
In[]:=
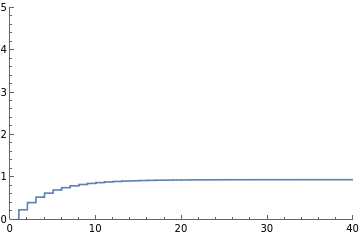
sumOfInterest[n_]:=Sum[1/2-sumA[m],{m,1,n}]Plot[sumOfInterest[n],{n,0,40},PlotRange{{0,40},{0,5}}]
Out[]=