Non-Sinusoidal Oscillation: A Balloon on a String

initial displacement

0.1

mass per unit length of string

0.05

gravitational acceleration

1.5

balloon volume

3

damping constant

0.02

run

Picture a buoyant balloon trailing a string with some mass per unit length. As the balloon rises, more string is lifted off the floor and the weight of the balloon-string system increases. As the balloon sinks, string returns to the floor and the weight of the balloon-string system decreases. In effect, the mass of the system depends on its position.

Details

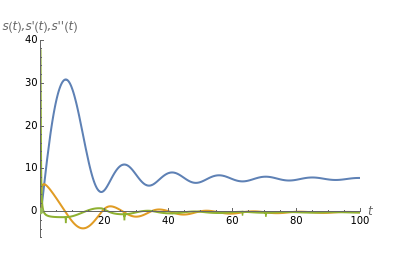
Snapshot 1: no damping; the displacement curve

s(t)

(blue) might look like a simple harmonic oscillator at first glance, but look at its derivatives

s'(t)

and

s''(t)

; note that energy is not conserved even in the absence of damping, as the rope is making inelastic collisions with the floor

Snapshot 2: massless string (and no damping); up, up, and away: in this case, the balloon is under the constant acceleration of its own lift

Snapshot 3: heavy string, small balloon, significant damping; the balloon reaches equilibrium around

t=50

External Links

Harmonic (ScienceWorld)

Oscillation (Wolfram MathWorld)

Standing Wave (ScienceWorld)

Permanent Citation

Dillon Tracy, Mark Robertson-Tessi

"Non-Sinusoidal Oscillation: A Balloon on a String"
http://demonstrations.wolfram.com/NonSinusoidalOscillationABalloonOnAString/
Wolfram Demonstrations Project
Published: March 14, 2008