Using Zeta Zeros to Compute the Mertens Function
Using Zeta Zeros to Compute the Mertens Function
The Mertens function, usually denoted by , is important in number theory. It is related to the famous unsolved Riemann hypothesis. The graph of is an irregular step function.
M(x)
M(x)
This Demonstration illustrates the remarkable fact that we can approximate the jumps of this irregular step function by using a sum that involves zeros of the Riemann function .
ζ(s)
Details
Details
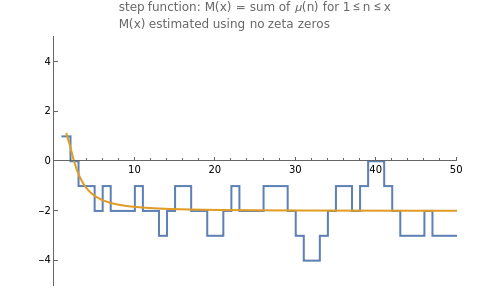
Snapshot 1: the graphs of the step function and the formula using no zeta zeros
M(x)
Snapshot 2: the graphs of and the formula using 40 pairs of zeta zeros
M(x)
The Moebius mu function is defined to be 1 if ; it is if is the product of distinct primes and 0 otherwise (i.e., if is divisible by the square of a prime).
μ(n)
n=1
k
(-1)
n
k
n
The Mertens function is defined to be the sum of for positive integers , μ(n).
M(x)
μ(n)
n≤x
∑
n≤x
The first three complex zeros of the zeta function are approximately , , and . The zeros occur in conjugate pairs, so if is a zero, then so is . The important Riemann hypothesis is the unproven conjecture that all these complex zeros have real part 1/2. So far, it has been verified that the first complex zeros do, indeed, have real part 1/2 (see[1]).
1/2+14.135i
1/2+21.022i
1/2+25.011i
a+bi
a-bi
13
10
In 1897, Mertens conjectured that for , is always between and . If the Mertens conjecture were true, then the Riemann hypothesis would be also have to be true. But in 1985, Odlyzko and te Riele[3] proved that the Mertens conjecture is false. This does not disprove the Riemann hypothesis, which remains one of the most important unsolved problems in mathematics.
x>1
M(x)
-
x
+
x
Odlyzko and te Riele did not give a specific for which the Mertens conjecture is false. However, in 2006, Kotnik and te Riele[2] proved that there is some for which the Mertens conjecture is false. It is also known[2] that the Mertens conjecture is true for all .
x
x<1.59×
40
10
x<
14
10
This Demonstration uses the following formula to calculate :
M(x)
M(x)≃-2+2Re()+
N
∑
k=1
ρ
k
x
ρ
k
′
ζ
ρ
k
∞
∑
k=1
-2k
x
(-2k)(-2k)
′
ζ
where is the complex zero of the Riemann zeta function. For a proof, see[4].
ρ
k
th
k
The first sum runs over the first complex zeros of the zeta function.
N
These complex zeros occur in conjugate pairs: if is a zero, then so is .
a+bi
a-bi
If you use the slider to choose, say, one pair of zeta zeros, then the first sum in the above formula, in effect, combines two terms corresponding to the first conjugate pair of zeta zeros and . So, when these terms are added, their imaginary parts cancel while their real parts add. The applied to the first sum is simply an efficient way to combine the two terms for each pair of zeta zeros.
1/2+14.135i
1/2-14.135i
2Re(…)
Notice that the second sum has the same form as the first, except that the second sum extends over the so-called "trivial" zeros of the zeta function, namely, . The second sum is small when is large. Notice that, without any zeta zeros being included (), this formula is close to when is large.
-2k=-2,-4,-6,…
x
N=0
-2
x
As we include more zeta zeros in the first sum, we more closely replicate the jumps in the step function , and we can do so for larger values of .
M(x)
x
All known zeta zeros have multiplicity 1, which is assumed in the formula. At those values of where jumps from to , the formula converges to the midpoint, , as approaches infinity. You can see this in the graphs.
x
M(x)
y=a
y=b
y=(a+b)/2
N
References
References
[2] T. Kotnik and H. J. J. te Riele, "The Mertens Conjecture Revisited," in Lecture Notes in Computer Science 4076, Proceedings of the 7th Algorithmic Number Theory Symposium, Berlin, 2006 pp. 156–167.
[3] A. M. Odlyzko and H. J. J. te Riele, "Disproof of the Mertens Conjecture," J. reine angew. Math. 357, 1985 pp. 138–160.
[4] E. C. Titchmarsh, The Theory of the Riemann Zeta-Function, Oxford: Clarendon Press, 1951 p. 318.
External Links
External Links
Permanent Citation
Permanent Citation
Robert Baillie
"Using Zeta Zeros to Compute the Mertens Function"
http://demonstrations.wolfram.com/UsingZetaZerosToComputeTheMertensFunction/
Wolfram Demonstrations Project
Published: March 7, 2011