Ptolemy's Table of Chords

table

picture

semicircle

page number

1

2

3

4

αº

40

partes	m	2
41	2	33

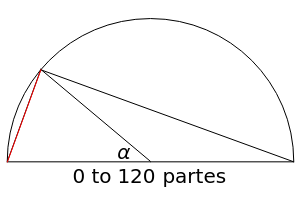
This Demonstration shows a reconstruction of Ptolemy's table of chords. He used 120 partes as the diameter of a circle. The chord is the red line in the semicircle. In modern terms, the table shows the values of

chord(αº)=120sin(αº/2)

as

αº

goes from 1/2º to 180º. The fractional parts of the chord lengths were expressed in sexagesimal (base 60) notation. After the columns for the arc and the chord (partes for integer part,

m

for 1/60, 2 for 1/3600), a third column is labeled "sixtieths" (

m

for integer part, 2 for 1/60, 3 for 1/3600), calculated by

2chord

2αº+1

2

-chord(αº)

. In the semicircle diagram,

α

runs from 0 to 120 partes.

Example:

chord(10º)=120sin(5º)≈10.4587≈10+27/60+31/3600

.

Details

The Demonstration reconstructs the table from the Latin version called Almagestum (1515). There are a few differences of one unit between the original and the reconstruction. This makes the accuracy of the table 1/3600.

References

[1] Wikipedia. "Ptolemy's Table of Chords." (Jan 5, 2016) en.wikipedia.org/wiki/Ptolemy's_table _of _chords.

External Links

Chord (Wolfram MathWorld)

Trigonometric Functions (Wolfram MathWorld)

Permanent Citation

Izidor Hafner

"Ptolemy's Table of Chords"
http://demonstrations.wolfram.com/PtolemysTableOfChords/
Wolfram Demonstrations Project
Published: January 6, 2016