Recursion in the Ackermann Function
Recursion in the Ackermann Function
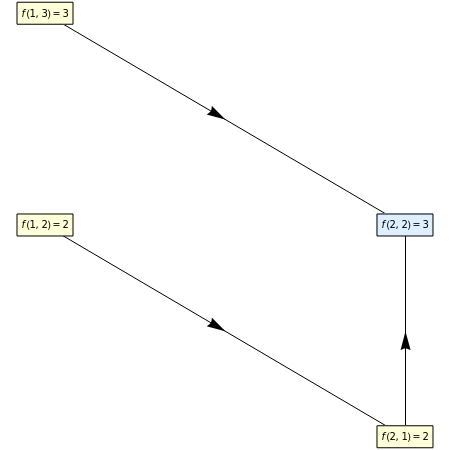
The Ackermann function is a classic example of a function that is not "primitive recursive"—its evaluation cannot be "unwound" into simple loops. See how instances of the Ackermann function get evaluated by calling on others. The Ackermann function grows very rapidly. As its first argument increases, it effectively goes from addition, to multiplication, powers, power towers, etc.
Details
Details
The definition used here is
f(1,n)=nf(m,1)=f(m-1,2)f(m,n)=f(m-1,f(m,n-1)+1),
which is a slight modification of Wilhelm Ackermann's original 1926 function.
External Links
External Links
Permanent Citation
Permanent Citation
Stephen Wolfram
"Recursion in the Ackermann Function"
http://demonstrations.wolfram.com/RecursionInTheAckermannFunction/
Wolfram Demonstrations Project
Published: September 28, 2007