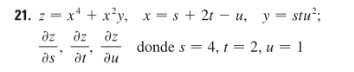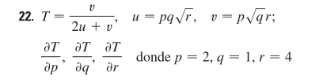In[]:=
(*Utilidadparamostrarderivadasenformacompacta*)derivs[f_,vars_List]:=Row@Riffle[TraditionalForm/@(HoldForm[D[f,#]]&/@vars),", "];​​​​(*Encabezadoprincipal*)​​Style["21–26 Use la regla de la cadena para calcular las derivadas parciales que se indican.",Bold,15]​​​​(*Listadeejerciciosconestructura*)​​Grid[{{"21.",Column[{Row[{TraditionalForm[z==x^4+x^2y],"; ",TraditionalForm[x==s+2t-u],"; ",TraditionalForm[y==stu^2]}],Row[{" ",derivs[z,{s,t,u}]}],Row[{" ",Style["donde ",Italic],TraditionalForm/@{s==4,t==2,u==1}//Row}]}]},{"22.",Column[{Row[{TraditionalForm[T==v/(2u+v)],"; ",TraditionalForm[u==pqSqrt[r]],"; ",TraditionalForm[v==pSqrt[qr]]}],Row[{" ",derivs[T,{p,q,r}]}],Row[{" ",Style["donde ",Italic],TraditionalForm/@{p==2,q==1,r==4}//Row}]}]},{"23.",Column[{Row[{TraditionalForm[w==xy+yz+zx],"; ",TraditionalForm[x==rCos[θ]],"; ",TraditionalForm[y==rSin[θ]],"; ",TraditionalForm[z==rθ]}],Row[{" ",derivs[w,{r,θ}]}],Row[{" ",Style["donde ",Italic],TraditionalForm/@{r==2,θ==π/2}//Row}]}]},{"24.",Column[{Row[{TraditionalForm[P==Sqrt[u^2+v^2+w^2]],"; ",TraditionalForm[u==xE^y],"; ",TraditionalForm[v==yE^x],"; ",TraditionalForm[w==E^(xy)]}],Row[{" ",derivs[P,{x,y}]}],Row[{" ",Style["donde ",Italic],TraditionalForm/@{x==0,y==2}//Row}]}]},{"25.",Column[{Row[{TraditionalForm[N==(p+q)/(p+r)],"; ",TraditionalForm[p==u+vw],"; ",TraditionalForm[q==v+uw],"; ",TraditionalForm[r==w+uw]}],Row[{" ",derivs[N,{u,v,w}]}],Row[{" ",Style["donde ",Italic],TraditionalForm/@{u==2,v==3,w==4}//Row}]}]},{"26.",Column[{Row[{TraditionalForm[u==xE^y],"; ",TraditionalForm[x==α^2β],"; ",TraditionalForm[y==β^2γ],"; ",TraditionalForm[t==γ^2α]}],Row[{" ",derivs[u,{α,β,γ}]}],Row[{" ",Style["donde ",Italic],TraditionalForm/@{α==-1,β==2,γ==1}//Row}]}]}},Alignment->{{Left,Left}},Spacings->{2,1},Frame->None]​​
Out[]=
21–26 Use la regla de la cadena para calcular las derivadas parciales que se indican.
Out[]=
21.
z
4
x
+
2
x
y; xs+2t-u; yst
2
u
∂z
∂s
,
∂z
∂t
,
∂z
∂u
donde s4t2u1
22.
T
v
2u+v
; upq
r
; vp
qr
∂T
∂p
,
∂T
∂q
,
∂T
∂r
donde p2q1r4
23.
wxy+xz+yz; xrcos(θ); yrsin(θ); zθr
∂w
∂r
,
∂w
∂θ
donde r2θ
π
2
24.
P
2
u
+
2
v
+
2
w
; ux
y

; v
x

y; w
xy

∂P
∂x
,
∂P
∂y
donde x0y2
25.
N
p+q
p+r
; pu+vw; quw+v; ruw+w
∂N
∂u
,
∂N
∂v
,
∂N
∂w
donde u2v3w4
26.
ux
y

; x
2
α
β; y
2
β
γ; tα
2
γ
∂u
∂α
,
∂u
∂β
,
∂u
∂γ
donde α-1β2γ1
In[]:=
(*Definicióndelasvariables*)ClearAll[z,x,y,s,t,u]​​​​x[s_,t_,u_]:=s+2t-u​​y[s_,t_,u_]:=stu^2​​z[s_,t_,u_]:=x[s,t,u]^4+x[s,t,u]^2*y[s,t,u]​​​​(*Derivadasparciales*)​​dzds=D[z[s,t,u],s];​​dzdt=D[z[s,t,u],t];​​dzdu=D[z[s,t,u],u];​​​​(*Mostrarlasderivadas*)​​dzds​​dzdt​​dzdu​​​​(*Evaluaciónenelpuntodado:s=4,t=2,u=1*)​​dzds/.{s->4,t->2,u->1}​​dzdt/.{s->4,t->2,u->1}​​dzdu/.{s->4,t->2,u->1}​​
Out[]=
4
3
(s+2t-u)
+2st(s+2t-u)
2
u
+t
2
(s+2t-u)
2
u
Out[]=
8
3
(s+2t-u)
+4st(s+2t-u)
2
u
+s
2
(s+2t-u)
2
u
Out[]=
-4
3
(s+2t-u)
+2st
2
(s+2t-u)
u-2st(s+2t-u)
2
u
Out[]=
1582
Out[]=
3164
Out[]=
-700
​
In[]:=
(*Definicióndelasvariables*)ClearAll[T,u,v,p,q,r];​​​​u[p_,q_,r_]:=p*q*Sqrt[r];​​v[p_,q_,r_]:=p*Sqrt[q]r;​​T[p_,q_,r_]:=v[p,q,r]/(2*u[p,q,r]+v[p,q,r]);​​​​(*Derivadasparciales(puedesdejarD[...]osimplificar)*)​​dTdp=D[T[p,q,r],p];​​dTdq=D[T[p,q,r],q];​​dTdr=D[T[p,q,r],r];​​​​(*Mostrarderivadassimbólicas*)​​dTdp​​dTdq​​dTdr​​​​(*Evaluaciónenelpuntodado:p=2,q=1,r=4*)​​pt={p->2,q->1,r->4};​​​​Print["El valor de ∂T/∂p en (2,1,4) es: ",dTdp/.pt];​​Print["El valor de ∂T/∂q en (2,1,4) es: ",dTdq/.pt];​​Print["El valor de ∂T/∂r en (2,1,4) es: ",dTdr/.pt];​​
Out[]=
-
p
q
r2q
r
+
q
r
2
2pq
r
+p
q
r
+
q
r
2pq
r
+p
q
r
Out[]=
-
p
q
r2p
r
+
pr
2
q
2
2pq
r
+p
q
r
+
pr
2
q
2pq
r
+p
q
r
Out[]=
-
p
q
p
q
+
pq
r
r
2
2pq
r
+p
q
r
+
p
q
2pq
r
+p
q
r
El valor de ∂T/∂p en (2,1,4) es: 0
El valor de ∂T/∂q en (2,1,4) es: -
1
8
El valor de ∂T/∂r en (2,1,4) es:
1
32
​