Wolfram Cloud Document

XMWUShortStrings[{"A""AA","A""BB","BAA""AB"},{"AAA"},12,5]

{{{AAA},1,{3,3}},{{AAAA,BBAA,ABBA,AABB},4,{4,4}},{{AAAAA,BBAAA,ABBAA,AABBA,AAABB,BBBBA,BAB,BBABB,ABBBB},9,{3,5}},{{BABA,ABAB,BAAB,BBBB},17,{4,6}},{{BABAA,ABABA,AABAB,BBBAB,BAABA,BABBB,ABAAB,BAAAB,ABB},30,{3,7}},{{},53,{6,8}},{{},97,{7,9}},{{},178,{8,10}},{{},327,{7,11}},{{},601,{8,12}},{{},1105,{9,13}},{{},2032,{10,14}},{{},3737,{11,15}}}

XMWUShortStrings[{"A""AA","A""BB","BAA""AB"},{"AABA"},8,5]

{{{AABA},1,{4,4}},{{AAABA,BBABA,ABBBA,AABAA,AABBB},5,{5,5}},{{AAAB},14,{4,6}},{{BABBA,AAAAB,BBAAB,ABBAB},31,{5,7}},{{BABB},64,{4,8}},{{BABAB,ABABB,BAABB,BBBBB},129,{5,9}},{{ABBB},250,{4,10}},{{},475,{7,11}},{{},899,{8,12}}}

XMWUShortStrings[{"A""AA","A""BB","BAA""AB"},{"A"},8,5]

{{{A},1,{1,1}},{{AA,BB},2,{2,2}},{{AAA,BBA,ABB},3,{3,3}},{{AAAA,BBAA,ABBA,AABB,BBBB},5,{4,4}},{{AAAAA,BBAAA,ABBAA,AABBA,AAABB,BBBBA,BAB,BBABB,ABBBB},9,{3,5}},{{BABA,ABAB,BAAB},16,{4,6}},{{BABAA,ABABA,AABAB,BBBAB,BAABA,BABBB,ABAAB,BAAAB},29,{5,7}},{{},53,{6,8}},{{},97,{7,9}}}

XMWUShortStrings[{"A""AA","A""BB","BBAA""AB"},{"A"},8,5]

{{{A},1,{1,1}},{{AA,BB},2,{2,2}},{{AAA,BBA,ABB},3,{3,3}},{{AAAA,BBAA,ABBA,AABB,BBBB},5,{4,4}},{{AAAAA,BBAAA,ABBAA,AABBA,AAABB,BBBBA,AB,BBABB,ABBBB},9,{2,5}},{{ABA,AAB,BBB},16,{3,6}},{{ABAA,AABA,AAAB,BBAB,BBBA,ABBB},27,{4,7}},{{ABAAA,AABAA,AAABA,AAAAB,BBABA,BBBAA,ABBBA,ABABB,BBAAB,ABBAB,AABBB,BBBBB},46,{5,8}},{{BAB},79,{3,9}}}

XMWUShortStrings[{"A""AA","A""BB","BBAA""AB"},{"A"},12,5]

{{{A},1,{1,1}},{{AA,BB},2,{2,2}},{{AAA,BBA,ABB},3,{3,3}},{{AAAA,BBAA,ABBA,AABB,BBBB},5,{4,4}},{{AAAAA,BBAAA,ABBAA,AABBA,AAABB,BBBBA,AB,BBABB,ABBBB},9,{2,5}},{{ABA,AAB,BBB},16,{3,6}},{{ABAA,AABA,AAAB,BBAB,BBBA,ABBB},27,{4,7}},{{ABAAA,AABAA,AAABA,AAAAB,BBABA,BBBAA,ABBBA,ABABB,BBAAB,ABBAB,AABBB,BBBBB},46,{5,8}},{{BAB},79,{3,9}},{{BABA,ABAB,BAAB},135,{4,10}},{{BABAA,ABABA,ABAAB,AABAB,BBBAB,BAABA,BABBB,BAAAB},231,{5,11}},{{},395,{6,12}},{{BABB},676,{4,13}}}

XMWUShortStrings[{"A""AA","A""BB","BBAA""AB"},{"AA"},12,5]

{{{AA},1,{2,2}},{{AAA,BBA,ABB},3,{3,3}},{{AAAA,BBAA,ABBA,AABB,BBBB},5,{4,4}},{{AAAAA,BBAAA,ABBAA,AABBA,AAABB,BBBBA,AB,BBABB,ABBBB},9,{2,5}},{{ABA,AAB,BBB},16,{3,6}},{{ABAA,AABA,AAAB,BBAB,BBBA,ABBB},27,{4,7}},{{ABAAA,AABAA,AAABA,AAAAB,BBABA,BBBAA,ABBBA,ABABB,BBAAB,ABBAB,AABBB,BBBBB},46,{5,8}},{{BAB},79,{3,9}},{{BABA,ABAB,BAAB},135,{4,10}},{{BABAA,ABABA,ABAAB,AABAB,BBBAB,BAABA,BABBB,BAAAB},231,{5,11}},{{},395,{6,12}},{{BABB},676,{4,13}},{{BABAB,BABBA,BAABB},1156,{5,14}}}

XMWUShortStrings[{"A""AA","A""BB","BBAA""AB"},{"AA"},14,5]

{{{AA},1,{2,2}},{{AAA,BBA,ABB},3,{3,3}},{{AAAA,BBAA,ABBA,AABB,BBBB},5,{4,4}},{{AAAAA,BBAAA,ABBAA,AABBA,AAABB,BBBBA,AB,BBABB,ABBBB},9,{2,5}},{{ABA,AAB,BBB},16,{3,6}},{{ABAA,AABA,AAAB,BBAB,BBBA,ABBB},27,{4,7}},{{ABAAA,AABAA,AAABA,AAAAB,BBABA,BBBAA,ABBBA,ABABB,BBAAB,ABBAB,AABBB,BBBBB},46,{5,8}},{{BAB},79,{3,9}},{{BABA,ABAB,BAAB},135,{4,10}},{{BABAA,ABABA,ABAAB,AABAB,BBBAB,BAABA,BABBB,BAAAB},231,{5,11}},{{},395,{6,12}},{{BABB},676,{4,13}},{{BABAB,BABBA,BAABB},1156,{5,14}},{{},1976,{6,15}},{{},3377,{7,16}}}

XMWUShortStrings[{"A""AA","A""BB","BBAA""AB"},{"ABA"},12,5]

{{{ABA},1,{3,3}},{{AABA,BBBA,ABAA,ABBB},4,{4,4}},{{AAABA,BBABA,ABBBA,AABAA,AABBB,BBBAA,BBBBB,ABAAA,ABABB},9,{5,5}},{{BAB},19,{3,6}},{{ABBA,ABAB,BABA,BAAB,BBBB},40,{4,7}},{{ABABA,AABBA,BBBBA,ABBAA,ABBBB,AABAB,BBBAB,ABAAB,BABAA,BAABA,BABBB,BAAAB},78,{5,8}},{{AAB},151,{3,9}},{{AAAB,BBAB,BABB},284,{4,10}},{{BABBA,AAAAB,BBAAB,ABBAB,BABAB,BAABB},524,{5,11}},{{ABB},957,{3,12}},{{AABB},1730,{4,13}},{{AAABB,BBABB},3108,{5,14}},{{},5551,{6,15}}}

XMWUShortStrings[{"A""AA","A""BB","BBAA""AB"},{"BBBAAB"},12,6]

{{{BBBAAB},1,{6,6}},{{BABB},4,{4,7}},{{BABAB,BAABB,BBBBB},8,{5,8}},{{BABAAB,BBBABB,BAABAB,BBBBAB,BABBBB,BAAABB},14,{6,9}},{{},25,{7,10}},{{BBABB,BABBB},46,{5,11}},{{BBABAB,BABABB,BABBAB,BBAABB,BBBBBB,BAABBB},83,{6,12}},{{ABBB},147,{4,13}},{{ABBAB,ABABB,AABBB},261,{5,14}},{{ABBAAB,BBABBB,ABABAB,AABBAB,ABBBBB,ABAABB,AABABB,AAABBB},462,{6,15}},{{AABB},815,{4,16}},{{AABAB,AAABB,ABBBB},1433,{5,17}},{{AABAAB,AAABAB,ABBABB,ABBBAB,AABBBB,AAAABB,ABABBB},2513,{6,18}}}

XMWUShortStrings[{"A""AA","A""BB","BBAA""AB"},{"BBBAA"},12,6]

{{{BBBAA},1,{5,5}},{{BBBAAA,BBBBBA,BAB,BBBABB},4,{3,6}},{{BABA,BAAB,BBBB},8,{4,7}},{{BABAA,BBBAB,BAABA,BBBBA,BABBB,BAAAB},14,{5,8}},{{BABAAA,BBBABA,BAABAA,BBBBAA,BABBBA,BABABB,BBBAAB,BBBBBB,BAAABA,BAABBB,BAAAAB,BABBAB},25,{6,9}},{{BBAB,BABB},46,{4,10}},{{BBABA,BABAB,BABBA,BBAAB,BBBBB,BAABB},83,{5,11}},{{BBABAA,BABABA,BABAAB,BABBAA,BBBBAB,BAABAB,BBAABA,BBABBB,BABBBB,BAABBA,BBAAAB,ABB,BAAABB},147,{3,12}},{{ABBA,ABAB,AABB},261,{4,13}},{{ABBAA,BBABB,ABABA,AABBA,ABBBB,ABAAB,AABAB,AAABB},462,{5,14}},{{ABBAAA,BBABAB,BBABBA,ABABAA,AABBAA,ABBBBA,AAB,ABBABB,BBAABB,ABAABA,AABABA,ABABBB,AAABBA,AABBBB,ABAAAB,AABAAB,ABBBAB,AAABAB,AAAABB},815,{3,15}},{{AABA,AAAB,ABBB},1433,{4,16}},{{AABAA,AAABA,ABBAB,ABBBA,AABBB,AAAAB,ABABB},2513,{5,17}}}

MWEvolveListTR[{"A""AA","A""BB","BBAA""AB"},{"A"},8];

Show[GraphicsRow[SMWXGraphics/@Take[Union[MWProofsTR[%200,"BAB"]],4]]];

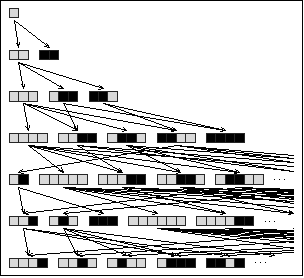
Show[MWCharRuleGraphic[{"A""AA","A""BB","BBAA""AB"}]];

Show[Surround[MWGraphic[MWEvolveListT[{"A""AA","A""BB","BBAA""AB"},{"A"},6],30]]];

XMWUShortStrings[{"A""AA","A""BB","BBAA""AB"},{"A"},8,5]

XMWUShortStrings[{"AB""BABA","ABAB""BB"},{"AABB"},8,5]

{{{AABB},1,{4,4}},{{},1,{6,6}},{{BBAB,ABBB},5,{4,8}},{{},8,{6,10}},{{BBBB},20,{4,12}},{{},37,{6,14}},{{},88,{8,16}},{{},184,{6,18}},{{},441,{8,20}}}

rrule={"A""AA","A""BB","BBAA""AB"};

etr=MWEvolveListTR[{"A""AA","A""BB","BBAA""AB"},{"AA"},12];

etr=MWEvolveListTR[{"A""AA","A""BB","BBAA""AB"},{"A"},7];

MWEvolveListTR[{"A""AA","A""BB","BBAA""AB"},{"A"},8];

Position[%25,"BAB"]

FindStepNumber[rule_,init_,find_,max_]:=Position[XMWUShortStrings[rule,init,max,StringLength[find]],find][[1,1]]-1

FindStepNumber[rrule,{"AA"},"BAB",10]

7

MakeProofs[rule_,init_,find_,max_]:=MWProofsTR[MWEvolveListTR[rule,{init},FindStepNumber[rule,{init},find,max]],find]

Show[SMWXGraphics[First[MakeProofs[rrule,"AA","BAB",10]]]];

Global`MWProofsTR