Rectifying an Alcohol-Water Mixture with Variable Enthalpies
Rectifying an Alcohol-Water Mixture with Variable Enthalpies
Rectification is a distillation process that produces a maximum concentration of ethanol in a mixture with water. In a traditional McCabe–Thiele analysis of a rectifying column studied in most undergraduate chemical engineering classes, it is assumed that the vapor and liquid enthalpies are independent of composition. The computations can then be done with a simple scientific calculator.
In this Demonstration, we relax the assumption of constant enthalpies and assume that the liquid and vapor enthalpies are linear functions of composition. This results in a nonconstant operating line for the rectifying column. (The operating line enforces the mathematical condition that the mass and energy of streams entering and leaving an equilibrium stage are conserved.) For this Demonstration, we consider an ethanol-water mixture that is to be enriched in a rectifying column. Vapor-liquid equilibrium data can be represented by the following piecewise functions:
y=
11.689x
1+13.21x
0≤x≤0.5
y=
0.702-0.408x
1-0.704x
0.5≤x≤1
x
y
Martin[1] gives the following enthalpy-composition relationships for the vapor and liquid enthalpies: and (enthalpies are given in BTU/pound).
H=+y=1150-692y
b
v
m
v
h=+y=156-66x
b
l
m
l
The curved operating line resulting from the material and energy balance equations is given by:
y
n
x
n+1
x
n+1
y
n
where , , and .
a=(1-R)-+(1-R)+R(1-R)-+(1-R)+R
x
D
m
l
H
N
b
v
h
D
x
D
m
v
H
N
b
l
h
D
b=(1-R)+(R-1)(1-R)-+(1-R)+R
m
v
m
l
x
D
m
v
H
N
b
l
h
D
c=(-)+R(-)(1-R)-+(1-R)+R
x
D
b
l
b
v
x
D
b
v
b
l
x
D
m
v
H
N
b
l
h
D
Here, is the internal reflux ratio, =1150-692 (enthalpy of overhead vapor stream), =156-66 (enthalpy of distillate stream), and is the distillate composition.
R=/
L
r
V
N
H
N
x
D
h
D
x
D
x
D
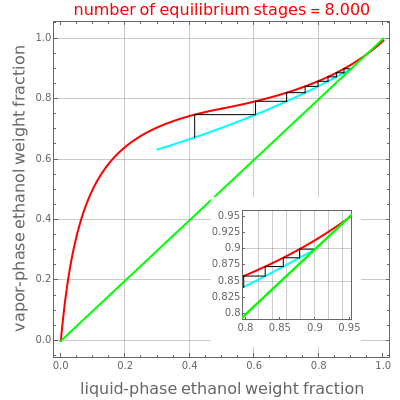
This Demonstration illustrates the step-off stages using alternately the equilibrium curve and the curved operating line, yielding the familiar staircase construction of a McCabe—Thiele diagram. In addition, the total number of theoretical equilibrium stages needed for the separation is calculated. You can set the values of: (1) the internal reflux ratio, ; (2) the distillate composition, ; and (3) the ethanol mass fraction in the liquid stream leaving at the bottom of the rectifying column, .
R
x
D
x
f
A comparison with rigorous results obtained with Aspen-HYSYS shows reasonable agreement, especially for high-ethanol weight fractions. Discrepancies are mainly due to the assumed VLE piecewise function and the enthalpy-composition functions.
When designing a rectification column, the fractional number representing the number of equilibrium stages needed to achieve the separation will in general be rounded up to the next higher integer value.
Details
Details
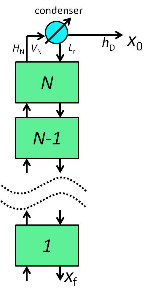
A schematic of the rectifying column is given below:
References
References
[1] J. J. Martin, " Analytical Solution of Equilibrium-Stage Operations—Application to Rectification with Varying Saturated Enthalpies and to Liquid-Liquid Extraction," AIChE Journal, 9(5), 1963 pp. 646–653. doi:10.1002/aic.690090515.
Permanent Citation
Permanent Citation
Housam Binous, Brian G. Higgins, Ahmed Bellagi
"Rectifying an Alcohol-Water Mixture with Variable Enthalpies"
http://demonstrations.wolfram.com/RectifyingAnAlcoholWaterMixtureWithVariableEnthalpies/
Wolfram Demonstrations Project
Published: February 15, 2013