Basic Parameters of the Kimberling Center X(55)
Basic Parameters of the Kimberling Center X(55)
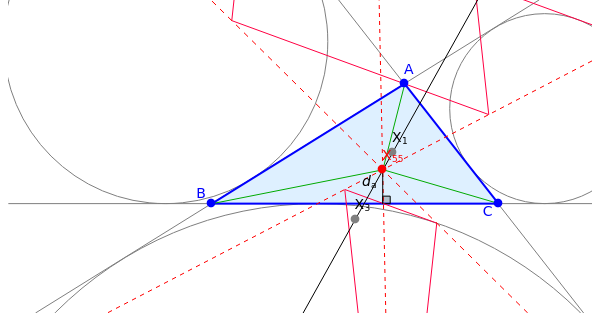
Given a triangle , the Kimberling center is the center of homothety of the tangential, intangents and extangents triangles[1].
ABC
X
55
The sides of the tangential triangle are tangent to the circumcircle of at , , . See the related links for the definitions of the intangents and extangents triangles.
ABC
A
B
C
The point is on the line , where and are the incenter and circumcenter of .
X
55
IO
I=
X
1
O=
X
3
ABC
Let
a
b
c
R
r
s
ABC
S=2ABC
d
a
d
b
d
c
X
55
ABC
d
X
55
d
a
d
b
d
c
Then
=
AX
55
R(bc(R+r)-Rr(4R+r))
R+r
d
a
a(s-a)
2(R+r)
d
X
55
r(4R+r)
R+r
You can drag the vertices , and .
A
B
C
Details
Details
A triangle center is said to be even when its barycentric coordinates can be expressed as a function of three variables , , that all occur with even exponents. If the center of a triangle has constant barycentric coordinates, it is called a neutral center (the centroid is the only neutral center). A triangle center is said to be odd if it is neither even nor neutral.
a
b
c
X
2
Standard barycentric coordinates of a point with respect to a reference triangle have a sum of 1.
References
References
[1] C. Kimberling. "Encyclopedia of Triangle Centers." (Jul 3, 2023) faculty.evansville.edu/ck6/encyclopedia.
External Links
External Links
Permanent Citation
Permanent Citation
Minh Trinh Xuan
"Basic Parameters of the Kimberling Center X(55)"
http://demonstrations.wolfram.com/BasicParametersOfTheKimberlingCenterX55/
Wolfram Demonstrations Project
Published: July 19, 2023