COVID-19 Progress in Peru Macro Regions: Coast vs. Mountain vs. Jungle
COVID-19 Progress in Peru Macro Regions: Coast vs. Mountain vs. Jungle
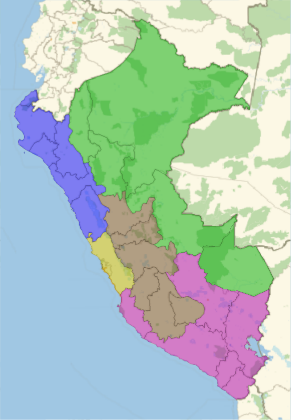
Macro Región Centro | DEPARTAMENTO |
Macro Región Norte | DEPARTAMENTO |
Macro Región Sur | DEPARTAMENTO |
Macro Región Oriente | DEPARTAMENTO |
Lima y Callao | DEPARTAMENTO |
departamentos de la costa | DEPARTAMENTO |
departamentos de la sierra | DEPARTAMENTO |
departamentos de la selva | DEPARTAMENTO |
Perú | DEPARTAMENTO |
Perú | DEPARTAMENTO |
Perú | DEPARTAMENTO |
Macro Región Centro | DEPARTAMENTO |
Macro Región Norte | DEPARTAMENTO |
Macro Región Sur | DEPARTAMENTO |
Macro Región Oriente | DEPARTAMENTO |
Lima y Callao | DEPARTAMENTO |
departamentos de la costa | DEPARTAMENTO |
departamentos de la sierra | DEPARTAMENTO |
departamentos de la selva | DEPARTAMENTO |
 |
|
 |
|