Performance Characteristics for Step Response of an Underdamped Process

steady-state gain

K

g

5

time constant τ

1

damping coefficient ζ

0.2

step magnitude M

5

response

performance

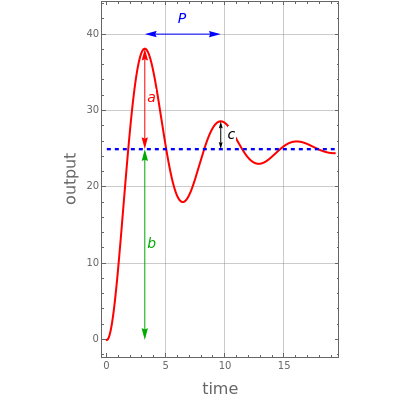
Consider an underdamped second-order process with a transfer function (the ratio of output to input of a system), given by

G(s)=

K

g

2

τ

2

s

+2ζτs+1

, where

K

g

is the steady-state gain,

τ

is the time constant, and

ζ

is the damping coefficient (with

0<ζ<1

). The process is subjected to a step input

U(t)=

M

s

. This Demonstration shows plots of the response

y(t)=

-1

ℒ

(G(s)U(s))

and finds its performance characteristics: overshoot

a/b

, decay ratio

c/a

, time to rise

t

r

, time to first peak

t

p

, and period of oscillations

P

. You can vary the values of

M

,

K

g

,

τ

, and

ζ

. Here, the values of

ζ

are restricted to the interval

[0.05,0.3]

in order to clearly identify

a

,

b

,

c

, and

P

in the plot of the output function

y(t)

.

Details

The overshoot is equal to

a/b=exp-πζ

1-

2

ζ



.

The decay ratio is equal to

c/a=

2

(a/b)

=exp-2πζ

1-

2

ζ



.

The period of oscillation is

P=2πτ

1-

2

ζ

.

The time to first peak is given by

t

p

=πτ

1-

2

ζ

.

The rise time is the solution

t

r

of

y(

t

r

)=M

K

g

and

0<

t

r

<

t

p

.

References

[1] D. E. Seborg, T. F. Edgar, D. A. Mellichamp, and F. J. Doyle III, Process Dynamics and Control, 3rd ed., New York: Wiley, 2011.

Permanent Citation

Housam Binous, Mohammad Mozahar Hossain, Ahmed Bellagi

"Performance Characteristics for Step Response of an Underdamped Process"
http://demonstrations.wolfram.com/PerformanceCharacteristicsForStepResponseOfAnUnderdampedProc/
Wolfram Demonstrations Project
Published: October 26, 2015