Concentration Profile in a Tubular Reactor

reactor length

15

reactor radius

0.5

diffusivity

0.005

axial velocity

0.5

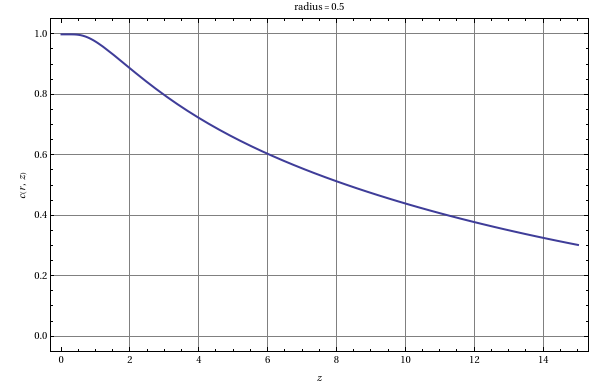
Consider a dilute solution with a solute concentration

c

0

, in laminar flow. This enters a tubular reactor with a catalytic wall that instantaneously and irreversibly converts the solute to its isomer. The system can be described by the equation [1]:

v

max

1-

2

r

R

∂c

∂z

=

1

r

∂

∂r

r

∂c

∂r

.

Assume that axial diffusion can be neglected in comparison to axial convection. Here

v

max

is the maximum laminar parabolic velocity,

r

and

z

are the radial and axial coordinates, respectively,

R

is the reactor radius,

c

is the concentration of the newly formed isomer and  is the diffusion coefficient. The boundary conditions are:

c(r,0)=

c

0

,

c(R,z)=0

,

∂c(0,z)

∂r

=0

.

Models like the one described here are useful in obtaining mass transfer data on metallic surfaces in studies designed to prevent or retard the oxidation of iron.