Confidence Intervals for the Erlang Distribution
Confidence Intervals for the Erlang Distribution
This Demonstration shows confidence intervals obtained by simulation for the parameter in an probability distribution.
λ
Erlang(100,λ)
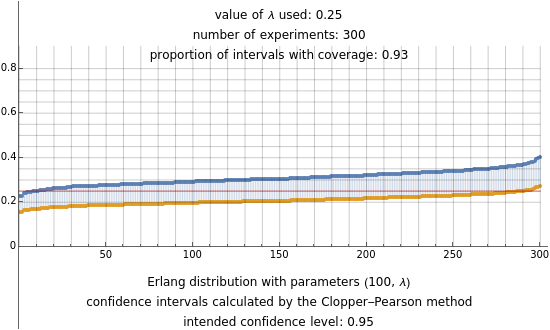
The probability distribution is defined as the distribution of the sum =+…+ of independent and identically distributed random variables ,…,, each distributed as Expλ (in Mathematica, ExponentialDistribution[λ]). In this case, the sum is sufficient to determine , that is, it contains all the information needed to compute any estimate of the parameter [1]. In this Demonstration, the Clopper–Pearson method [2, 3] is used to produce interval estimates for , assuming a fixed sample size of 100, and their behavior is shown experimentally using simulation to produce random intervals. In this manner it may be seen that the method behaves rather well, since the relative frequency of the generated intervals that contain the true value of the parameter is very close to (and often higher than) the theoretical confidence level. Three different values (0.25, 0.45 and 0.65) are used for the experiment.
Erlang(k,λ)
S
k
X
1
X
k
k
X
1
X
k
X
i
S
k
λ
λ