The Law of the Iterated Logarithm in Probability Theory
The Law of the Iterated Logarithm in Probability Theory
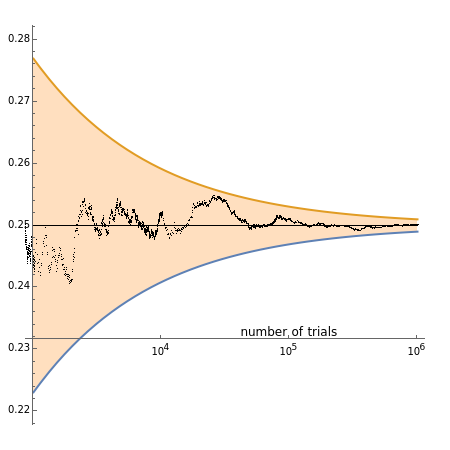
The law of the iterated logarithm is a refinement of the strong law of large numbers, a fundamental result in probability theory. In the particular case of an unlimited sequence of Bernoulli trials with parameter , the strong law asserts that with probability one, the relative frequency of successes converges to p as the number of trials grows.
p
The relative frequency of successes is simulated for 1,000,000 trials, and is plotted against a log scale for the number of trials. As the number of trials increases the relative frequency is observed to remain within the funnel-shaped region described by the law of the iterated logarithm, and only in rare cases will it land outside the funnel.
Move the slider to change the value of p and watch the behavior of the relative frequencies as a function of the number of trials. Open the control for the slider and use the "Play" animation control to repeat the process automatically for different values of .
p
Details
Details
The main reference for this topic is W. Feller, "Unlimited Sequences of Bernoulli Trials: The Law of the Iterated Logarithm," An Introduction to Probability Theory and Its Applications, Vol. 1, New York: John Wiley & Sons, Inc., 1970 pp. 204–208.
External Links
External Links
Permanent Citation
Permanent Citation
Tomas Garza
"The Law of the Iterated Logarithm in Probability Theory"
http://demonstrations.wolfram.com/TheLawOfTheIteratedLogarithmInProbabilityTheory/
Wolfram Demonstrations Project
Published: December 19, 2007