Permutation Notations
Permutation Notations
The number of ways to arrange seven objects in a row is . The arrangements are called permutations. Combinatorialists use two notational systems for permutations.
7=7×6×5×4×3×2×1=5040
The first notation has positions on top and numbers of the rearranged objects on the bottom. It can be read as a mapping of a finite set of numbers, where the numbers on top get mapped to those below.
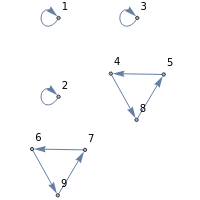
The second notation applies that mapping repeatedly to any starting number until there is a repetition. Then a new number is chosen to start the next cycle, and so on. A permutation can be shown as a directed graph.
External Links
External Links
Permanent Citation
Permanent Citation
Ed Pegg Jr
"Permutation Notations"
http://demonstrations.wolfram.com/PermutationNotations/
Wolfram Demonstrations Project
Published: April 27, 2007