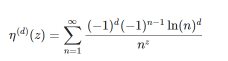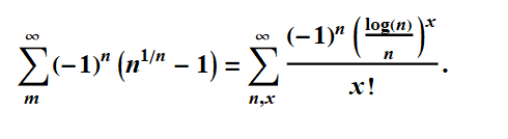CMRB=m=∞∑mn(-1)(1/nn-1)
CMRB=m=(-1)
∞
∑
m
n
(-1)
1/n
n
In[]:=
m=NSum[(-1)^n(n^(1/n)-1),{n,∞},WorkingPrecision100,PrecisionGoal200,Method"AlternatingSigns"]
Out[]=
0.18785964246206712024851793405427323005590309490013878617200468408947723156466021370329665443310750
Also consider the following.
In[]:=
c1=Log[2](-2EulerGamma+Log[2]);
1
2
In[]:=
m+(c1-NSum[Cos[Pin]/Gamma[1+x](Log[n]/n)^x,{n,2,Infinity},{x,2,60},Method"AlternatingSigns",WorkingPrecision100,NSumTerms200])
Out[]=
-3.9×
-97
10
=
∞
∑
n,x=2
cos(πn)
x
log(n)
n
Γ(x+1)
1
2
In[]:=
m-NSum[Cos[Pin]/Gamma[1+x](Log[n]/n)^x,{n,1,Infinity},{x,1,60},Method"AlternatingSigns",WorkingPrecision100,NSumTerms200]
Out[]=
-9.5087×
-94
10
In[]:=
m-NSum[Cos[Pin]/Gamma[1+x](Log[n]/n)^x,{n,1,Infinity},{x,1,60},Method"AlternatingSigns",WorkingPrecision100,NSumTerms200]
Out[]=
-9.5087×
-94
10