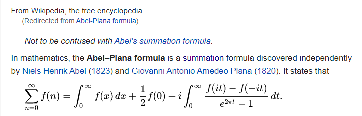
Some relationships between the MKB and the MRB constant
Some relationships between the MKB and the MRB constant
f(x)=1-
x
(-1)
1
x+1
(x+1)
h(x)=(-1)
x
(-1)
1/x
x
g(x)=
1/x
x
CMRB=f(n)=f(n)=h(n)
∞
∑
n=0
∞
∑
n=1
∞
∑
n=1
MKB=g(t)t=-t+
N∞
2N+1
∫
1
πt
∞
∫
0
g(1+t)
πt
π
((f(t)-f(-t))/(-1))t+g(t)t=CMRB
∞
∫
0
2πt
N∞
2N+1
∫
1
πt
In[]:=
f(x_)=1-;h(x_)=(-1);g(x_)=;
x
(-1)
1
x+1
(x+1)
x
(-1)
1/x
x
1/x
x
In[]:=
NIntegrate[E^(Pi*I*t)*g[t],{t,1,10001},WorkingPrecision->10]
Out[]=
0.07079022316-0.04706930965
In[]:=
MKB=-INIntegrate[g[1+It]/E^(Pit),{t,0,Infinity},WorkingPrecision100,MaxRecursion20]-I/Pi
Out[]=
0.0707760393115288035395280218302820013657546962033630275831727881636184572643820365808318812661772382-0.6840003894379321291827444599926611267109914826549994343226303771381530581249766381509598342127214787
In[]:=
CMRB=NSum[h[n],{n,1,Infinity},Method"AlternatingSigns",WorkingPrecision100];
In[]:=
term=NIntegrate[((I(f[It]-f[-It])))/(E^(2Pit)-1),{t,0,Infinity},WorkingPrecision100,Method"GlobalAdaptive"]
Out[]=
0.11708360315053831670898991222399122869014839869677575858883189592585877430027817712246477316693025869+0.04738061707035078610720940650260367857315289969317363933196100090256586758807049779050462314770913485
In[]:=
(term+MKB-CMRB)
Out[]=
9.3472×+0.×
-94
10
-101
10
In[]:=
NoMKB=It.
∞
∫
0
h(1-t)-h(1+t)
exp(2πt)-1
In[]:=
NoMKB=Im[NIntegrate[(h[(1-It)]-h[(1+It)])/(Exp[2Pit]-1),{t,0,Infinity},WorkingPrecision100]]
Out[]=
0.11708360315053831670898991222399122869014839869677575858883189592585877430027817712246477316693025869
In[]:=
NoMKB+Re[MKB]-CMRB
Out[]=
9.3472×
-94
10
In[]:=
term+2I/Pi
Out[]=
0.11708360315053831670898991222399122869014839869677575858883189592585877430027817712246477316693025869+0.68400038943793212918274445999266112671099148265499943432263037713815305812497663815095983421272147867
∞
∫
0
(h(1+t)-h(1-t))
2πt
2
π
∞
∫
0
(f(t)-f(-t))
2πt
In[]:=
-NIntegrate[((I(h[1+It]-h[1-It])))/(E^(2Pit)-1),{t,0,Infinity},WorkingPrecision100,Method"GlobalAdaptive"]-2I/Pi
Out[]=
-0.11708360315053831670898991222399122869014839869677575858883189592585877430027817712246477316693025869-0.68400038943793212918274445999266112671099148265499943432263037713815305812497663815095983421272147867
In[]:=
NoMKB+Im[MKB]I
Out[]=
0.11708360315053831670898991222399122869014839869677575858883189592585877430027817712246477316693025869-0.6840003894379321291827444599926611267109914826549994343226303771381530581249766381509598342127214787
-1t==-1==term
∞
∫
0
(h(1+t)-h(1-t))
2πt
∞
∫
0
(f(t)-f(-t))
2πt
In[]:=
term-NIntegrate[((I(h[1+It]-h[1-It])))/(E^(2Pit)-1),{t,0,Infinity},WorkingPrecision100,Method"GlobalAdaptive"]
Out[]=
0.×+0.×
-101
10
-101
10
In[]:=
NIntegrate[((I(f[It]-f[-It])))/(E^(2Pit)-1),{t,0,Infinity},WorkingPrecision100,Method"GlobalAdaptive"]-term
Out[]=
0.×+0.×
-101
10
-101
10
In[]:=
MKB
Out[]=
0.0707760393115288035395280218302820013657546962033630275831727881636184572643820365808318812661772382-0.6840003894379321291827444599926611267109914826549994343226303771381530581249766381509598342127214787