Perceived equal steps in size for disks
May 2023, Nick Holliman.
A mathematical interpretation of this paper:
‘A model of symbol size discrimination in scatterplots.’ Li, J., Martens, J.B. and van Wijk, J.J., 2010, April.
In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (pp. 2553-2562).
Summary of findings:
Is size judgement a judgement of length or area?
Previous work:
Larger size differences result in larger separation difference
Separation distances between larger symbols are relatively smaller then between smaller ones.
Equal size differences do not result in equal separation and it is harder to separate larger symbols.
Assume symbols are separated by perceived strength not by physical difference.
G converts physical to perceived, and in perceived space equal steps should mean equal separability.
P= G(r)
Exp 1 Circles with radii i * r0 where i = 1,...,8 and r0 = 0.625mm (we normalise radii on a scale of 0.0-1.0 below)
Exp 2 Equal visual separability, β = 0.4.
[NB: Follow on work suggests a better result using β = 0.7 (essentially Steven’s law):
Perception of means, sums, and areas. Raidvee, A., Toom, M., Averin, K. et al.
Atten Percept Psychophys 82, 865–876 (2020). https://doi.org/10.3758/s13414-019-01938-7 ]
May 2023, Nick Holliman.
A mathematical interpretation of this paper:
‘A model of symbol size discrimination in scatterplots.’ Li, J., Martens, J.B. and van Wijk, J.J., 2010, April.
In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (pp. 2553-2562).
Summary of findings:
Is size judgement a judgement of length or area?
Previous work:
Larger size differences result in larger separation difference
Separation distances between larger symbols are relatively smaller then between smaller ones.
Equal size differences do not result in equal separation and it is harder to separate larger symbols.
Assume symbols are separated by perceived strength not by physical difference.
G converts physical to perceived, and in perceived space equal steps should mean equal separability.
P= G(r)
Exp 1 Circles with radii i * r0 where i = 1,...,8 and r0 = 0.625mm (we normalise radii on a scale of 0.0-1.0 below)
Exp 2 Equal visual separability, β = 0.4.
[NB: Follow on work suggests a better result using β = 0.7 (essentially Steven’s law):
Perception of means, sums, and areas. Raidvee, A., Toom, M., Averin, K. et al.
Atten Percept Psychophys 82, 865–876 (2020). https://doi.org/10.3758/s13414-019-01938-7 ]
In[]:=
A model to determine equal size steps between disk shapes.
GG gives the perceived size of a shape given the physical drawn radius r.
The research in Li found that β of approx 0.4 gives a good approximation to perception.
α is a constant scaling factor to scale the drawings, which we assume here is equal to one.
GG gives the perceived size of a shape given the physical drawn radius r.
The research in Li found that β of approx 0.4 gives a good approximation to perception.
α is a constant scaling factor to scale the drawings, which we assume here is equal to one.
In[]:=
GG[r_,γ_]:=Module[{β=γ,α=1},α]
β
r
The inverse function, find the drawn radius of the shape given the perceived radius
In[]:=
GGinv[P_,γ_]:=Module[{β=γ,α=1},α]
1/β
P
Draw eight shapes as in the original paper.
(In the paper a linear sequence went from = 0.625mm, in equal steps to = 5.0mm)
If the largest shape has a perceived radius of P = 1.0.
We want the smallest to be perceived eight times smaller P= 0.125.
Now interpolate in P space and find the corresponding r values in physical space.
(In the paper a linear sequence went from
r
0
r
max
If the largest shape has a perceived radius of P = 1.0.
We want the smallest to be perceived eight times smaller P= 0.125.
Now interpolate in P space and find the corresponding r values in physical space.
In[]:=
smallestPerceivedRadius=0.125;largestPerceivedRadius=1.0;
Calculate the step size of the drawn shapes so they are perceived to be equally different.
In[]:=
step=(largestPerceivedRadius-smallestPerceivedRadius)/7
Out[]=
0.125
In[]:=
equalPerceived=Range[smallestPerceivedRadius,largestPerceivedRadius,step]
Out[]=
{0.125,0.25,0.375,0.5,0.625,0.75,0.875,1.}
In[]:=
expβ=0.4;drawnAs04=GGinv[equalPerceived[[#]],expβ]&/@Range[1,8]drawnAs07=GGinv[equalPerceived[[#]],0.7]&/@Range[1,8]drawnAs10=GGinv[equalPerceived[[#]],1.0]&/@Range[1,8]drawnAs14=GGinv[equalPerceived[[#]],1.4]&/@Range[1,8]drawnAs20=GGinv[equalPerceived[[#]],2.0]&/@Range[1,8]drawnAs25=GGinv[equalPerceived[[#]],2.5]&/@Range[1,8]
Out[]=
{0.00552427,0.03125,0.0861149,0.176777,0.308816,0.487139,0.716177,1.}
Out[]=
{0.051271,0.138011,0.246305,0.371499,0.510975,0.663004,0.826332,1.}
Out[]=
{0.125,0.25,0.375,0.5,0.625,0.75,0.875,1.}
Out[]=
{0.226431,0.371499,0.496291,0.609507,0.714825,0.814251,0.909028,1.}
Out[]=
{0.353553,0.5,0.612372,0.707107,0.790569,0.866025,0.935414,1.}
Out[]=
{0.435275,0.574349,0.67548,0.757858,0.828614,0.891301,0.947989,1.}
In[]:=
In[]:=
xScale=22;sizeScale=10;plotNames={"β = "<>ToString[expβ],"β = 0.7","β = 1.0","β = 1.4","β = 2.0","β = 2.4"};gfxList=Graphics[{Disk[{#*xScale,0},drawnAs04[[#]]*sizeScale]&/@Range[1,8],Text[plotNames[[1]],{9*xScale,0}]}]gfxList=Graphics[{Disk[{#*xScale,0},drawnAs07[[#]]*sizeScale]&/@Range[1,8],Text[plotNames[[2]],{9*xScale,0}]}]gfxList=Graphics[{Disk[{#*xScale,0},drawnAs10[[#]]*sizeScale]&/@Range[1,8],Text[plotNames[[3]],{9*xScale,0}]}]gfxList=Graphics[{Disk[{#*xScale,0},drawnAs14[[#]]*sizeScale]&/@Range[1,8],Text[plotNames[[4]],{9*xScale,0}]}]gfxList=Graphics[{Disk[{#*xScale,0},drawnAs20[[#]]*sizeScale]&/@Range[1,8],Text[plotNames[[5]],{9*xScale,0}]}]gfxList=Graphics[{Disk[{#*xScale,0},drawnAs25[[#]]*sizeScale]&/@Range[1,8],Text[plotNames[[6]],{9*xScale,0}]}]
Out[]=
Out[]=
Out[]=
Out[]=
Out[]=
Out[]=
In[]:=
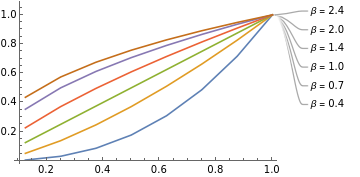
ListLinePlot[{Transpose@{equalPerceived,drawnAs04},Transpose@{equalPerceived,drawnAs07},Transpose@{equalPerceived,drawnAs10},Transpose@{equalPerceived,drawnAs14},Transpose@{equalPerceived,drawnAs20},Transpose@{equalPerceived,drawnAs25}},PlotRange->All,PlotLabels->plotNames]
Out[]=
The x-axis above is the perceived size, the goal is to achieve equal steps in perceived size.
The y-axis is the size drawn given different values of β to achieve linear perception.
The Li 2010 paper concludes β of 0.4 gives perceived equal steps in size.
The more recent Raidvee 2020 work suggests that β of 0.7 has this result.
Both proposals increase the drawn size proportionally more for larger shapes.
The y-axis is the size drawn given different values of β to achieve linear perception.
The Li 2010 paper concludes β of 0.4 gives perceived equal steps in size.
The more recent Raidvee 2020 work suggests that β of 0.7 has this result.
Both proposals increase the drawn size proportionally more for larger shapes.
Open questions:
How big is an equal step in perceived size, it needs to be also clearly distinguishable.
With β = 0.4 there will be a more limited number of practical shape size steps available.
How do surrounding shapes affect the perception of other shapes.
How big is an equal step in perceived size, it needs to be also clearly distinguishable.
With β = 0.4 there will be a more limited number of practical shape size steps available.
How do surrounding shapes affect the perception of other shapes.