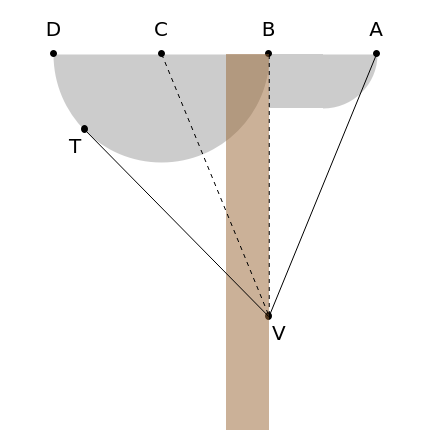
Tomahawk Trisection of an Angle

move V

2.44

Let

AB=BC=CD

. Let

σ

be a semicircle with diameter

BD

.

Given any angle

∠AVT

where

VT

is tangent to

σ

at

B

, the straight lines

VC

and

VB

trisect

∠AVT

.

In other words, the triangles

△VTC

,

△VBC

and

△VBA

are congruent.

Details

This Demonstration is based on[1]. The construction violates the Euclidean constraints on the use of only a straight edge and compass; specifically, by drawing the tangent

VT

. The result is true nonetheless since the semicircle radius

R=AB=BC=CT

and

X=CV=VA

. Then

sin∠AVB=sin∠BVC=sin∠CVT=R/X

.

References

[1] G. E. Martin, Geometric Constructions, New York: Springer, 1998 pp. 20–21.

External Links

Angle Trisection (Wolfram MathWorld)

Descartes's Angle Trisection

Pascal's Angle Trisection

Archimedes's Neusis Angle-Trisection

Permanent Citation

Izidor Hafner

"Tomahawk Trisection of an Angle"
http://demonstrations.wolfram.com/TomahawkTrisectionOfAnAngle/
Wolfram Demonstrations Project
Published: September 8, 2017