1992 CMO Problem: Cocircular Orthocenters

P

1

P

2

P

3

P

4

Let

P

1

,

P

2

,

P

3

,

P

4

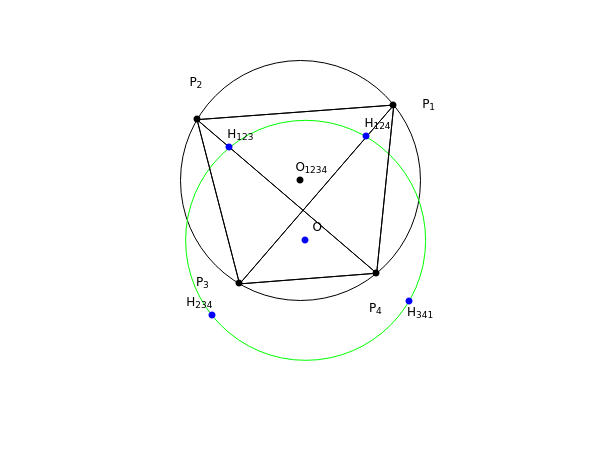
be distinct points on a circle (black) centered at

O

1234

. Let

H

123

be the orthocenter of triangle

P

1

P

2

P

3

and so on. You can show that the four orthocenters are cocircular and the circle (green) has the same radius as the original circle.

Details

This Demonstration is based on a problem from the 2nd Section of the Chinese Math Olympic National Final in 1992.

External Links

Cyclic Quadrilateral (Wolfram MathWorld)

Orthocenter (Wolfram MathWorld)

Permanent Citation

Shenghui Yang

"1992 CMO Problem: Cocircular Orthocenters" from the Wolfram Demonstrations Project http://demonstrations.wolfram.com/1992CMOProblemCocircularOrthocenters/
Published: June 18, 2012

© Wolfram Demonstrations Project & Contributors |Terms of Use