Distance between the Centers of the Nine-Point and Apollonius Circles

EE' 2 	R 9 + R a 2 ) 1- r R 9
1.76572	1.76572

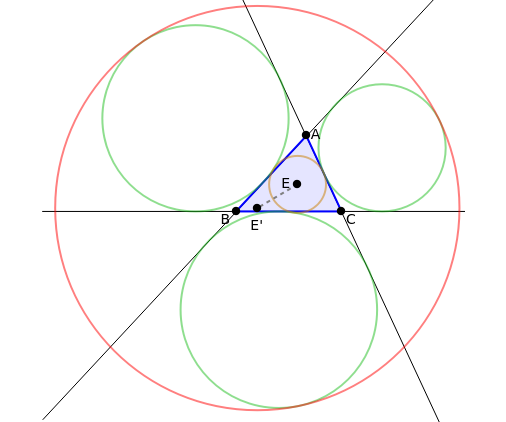
For a triangle

ABC

, let

R

and

r

be the circumradius and inradius,

s

be the semiperimeter,

⊙(E,

R

9

)

be the nine-point circle and

⊙(E',

R

a

)

be the Apollonius circle.

Then

R

9

=

R

2

,

R

a

=

2

r

+

2

s

4r

,

and

2

EE'

=

2

(

R

9

+

R

a

)

1-

r

R

9

.

You can drag the points

A

,

B

and

C

.

External Links

A Triangle Formed by the Centers of Three Nine-Point Circles

Nine-Point Circle

Nine-Point Center (Wolfram MathWorld)

Nine-Point Circle in the Complex Plane

Apollonius Circle (Wolfram MathWorld)

Radical Circle of Three Circles

Tetrahedron Centers

The Center and Radius of the Nine-Point Circle

Permanent Citation

Minh Trinh Xuan

"Distance between the Centers of the Nine-Point and Apollonius Circles"
http://demonstrations.wolfram.com/DistanceBetweenTheCentersOfTheNinePointAndApolloniusCircles/
Wolfram Demonstrations Project
Published: June 7, 2022