Lewis Carroll's Bilateral Diagram
Lewis Carroll's Bilateral Diagram
Aristotelian logic, or the traditional study of deduction, deals with four so-called categorical or subject-predicate propositions, which can be defined by:
S a P ⇔ All S is P (universal affirmative or A proposition),
S i P ⇔ Some S is P (particular affirmative or I proposition),
S e P ⇔ No S is P (universal negative or E proposition),
S o P ⇔ Some S is not P (particular negative or O proposition).
S a P ⇔ All S is P (universal affirmative or A proposition),
S i P ⇔ Some S is P (particular affirmative or I proposition),
S e P ⇔ No S is P (universal negative or E proposition),
S o P ⇔ Some S is not P (particular negative or O proposition).
S is called a subject (or minor) term and P is called a predicate (or major) term of a proposition. We could think of S and P as one-place predicates or sets.
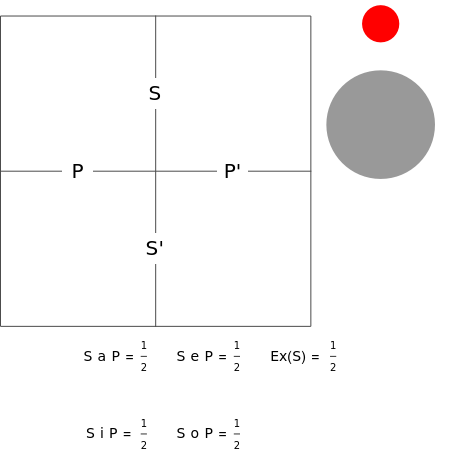
The bilateral diagram is a way to understand relations among categorical propositions. It
is a square divided into four smaller square cells: SP, SP', S'P, S'P'. A red counter (or 1) within a cell means that there is at least one thing in it. A gray counter (or 0) within a cell means there is nothing in it. So we may not put both counters in the same cell. A red counter in the cell SP means "Some S is P"; a gray counter in the cell SP means "No S is P". The red counter in the upper rectangle means that there is at least one S, symbolically Ex(S) ⇔ S i S. But if we put the counter on the common line of squares SP and SP', we don't know whether the proposition S i P is true (1) or false (0), so it has value unknown or undetermined (½). The same holds for S o P. Analogously, the value of the proposition S a P is ½, unless we put the gray counter in the square SP' (S a P = 1) or in SP (S a P = 0).
is a square divided into four smaller square cells: SP, SP', S'P, S'P'. A red counter (or 1) within a cell means that there is at least one thing in it. A gray counter (or 0) within a cell means there is nothing in it. So we may not put both counters in the same cell. A red counter in the cell SP means "Some S is P"; a gray counter in the cell SP means "No S is P". The red counter in the upper rectangle means that there is at least one S, symbolically Ex(S) ⇔ S i S. But if we put the counter on the common line of squares SP and SP', we don't know whether the proposition S i P is true (1) or false (0), so it has value unknown or undetermined (½). The same holds for S o P. Analogously, the value of the proposition S a P is ½, unless we put the gray counter in the square SP' (S a P = 1) or in SP (S a P = 0).
Details
Details
A diagram showing the relations among categorical propositions is known as the traditional square of opposition[2, p. 217]. Two propositions are contradictories if one is the negation of the other. Propositions A and O, and propositions I and E are contradictories. Two propositions are contraries if they cannot both be true. Two propositions are subcontraries if they cannot both be false. Proposition A is called superaltern, I is called subaltern, and the coresponding relation is called subalternation. The same definitions are aplied to E and O[2, pp. 214-217]. Under the assumption that class S is not empty, propositions A and E are contraries, propositions I and O are subcontraries, and superaltern implies subaltern.
[1] L. Carroll, Symbolic Logic and The Game of Logic, New York: Dover, 1958.
[2] I. M. Copi and C. Cohen, Introduction to Logic, 9th ed., New York: Macmillan, 1994 pp. 214-218.
External Links
External Links
Permanent Citation
Permanent Citation
Izidor Hafner
"Lewis Carroll's Bilateral Diagram"
http://demonstrations.wolfram.com/LewisCarrollsBilateralDiagram/
Wolfram Demonstrations Project
Published: March 7, 2011