A Converging Geometric Series
A Converging Geometric Series
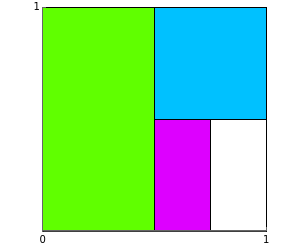
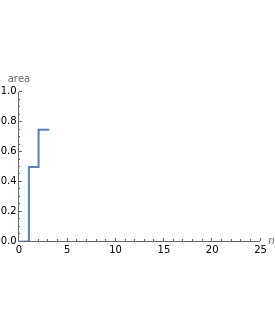
This Demonstration shows that =+++…+=1.
∞
∑
n=1
n
1
2
1
2
1
4
1
8
n
1
2
The square is half empty with area when . The square is empty at . In general, the square is empty at step and +++…+ full, which shows that converges to 1.
1
2
n=1
1
4
n=2
n
1
2
n
1
2
1
4
1
8
n
1
2
∞
∑
n=1
n
1
2
Details
Details
Snapshot 1: when , the area is filled is
n=1
1
2
Snapshot 2: when , a square with area == is added
n=4
n
1
2
4
1
2
1
16
Snapshot 3: where and the area filled is very close to 1
n=25
The geometric series converges if and only if , and then the sum of the series is . Convergence of can be proven by the integral test, which states that if is continuous, decreasing, and positive, then f(x) converges if f(x)dx converges. In this case, dx=, so the integral converges and therefore the geometric series also converges.
∞
∑
n=1
n
r
|r|<1
r
1-r
∞
∑
n=1
n
r
f(x)
∞
∑
n=1
∞
∫
1
∞
∫
1
x
1
2
1
ln[4]
Special thanks to the University of Illinois NetMath Program and the mathematics department at William Fremd High School.
References
References
[2] M. Moody. "Convergence Tests for Infinite Series." (Jun 18, 2013) www.math.hmc.edu/calculus/tutorials/convergence.
External Links
External Links
Permanent Citation
Permanent Citation
Akane Hattori, Natsuki Okuda
"A Converging Geometric Series"
http://demonstrations.wolfram.com/AConvergingGeometricSeries/
Wolfram Demonstrations Project
Published: June 19, 2013