N-Body Problem in 2D

time

bodies

4

random seed

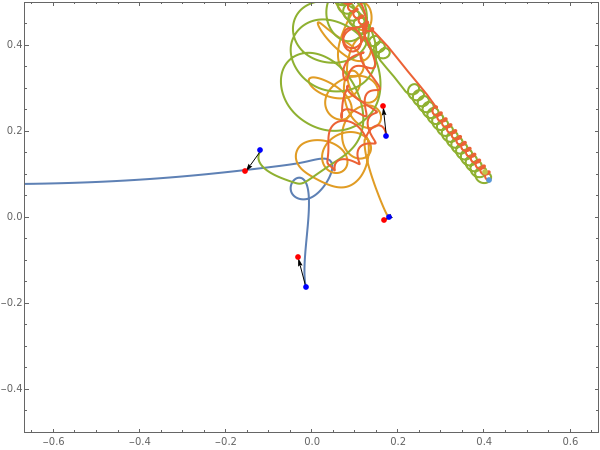
This Demonstration shows a two-dimensional version of the

N

-body problem, in which

N

different masses interact gravitationally. In order to predict their motions, a system of coupled differential equations must be solved consistent with a set of initial conditions for positions and velocities that are chosen at random.

Details

The equations of motion are:

..

r

i

=-g

n

∑

j=1,≠i

m

j

r

i

-

r

j



r

i

-

r

j

3

|

,

where

..

r

i

is the acceleration of the body

i

,

g

is the gravitational constant,

m

j

is the

th

j

mass, and

r

i

-

r

j

is the vector connecting masses

i

and

j

.

References

[1] M. Trenti and P. Hut, "N-Body Simulations (Gravitational)," Scholarpedia, 3(5):3930, 2008. www.scholarpedia.org/article/N-body_simulations _ %28 gravitational %29.

External Links

Velocity (ScienceWorld)

Acceleration (ScienceWorld)

Mass (ScienceWorld)

Gravitational Constant (ScienceWorld)

n-Body Problem (ScienceWorld)

Permanent Citation

Enrique Zeleny

"N-Body Problem in 2D"
http://demonstrations.wolfram.com/NBodyProblemIn2D/
Wolfram Demonstrations Project
Published: February 4, 2013